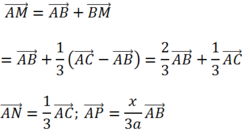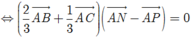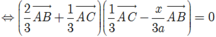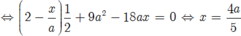cho tam giác ABC đều có cạnh 3a. Lấy các điểm M,N lần lượt trên cạnh BC,CA sao cho BM=a, CN=2a.Gọi P là điểm trên cạnh AB sao cho AM vuông gó với PN . Tính độ dài PN theo a
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
EN
1 tháng 8 2021
a) Vì O cách đều 3 cạnh của tam giác nên OD = OE = OF
Áp dụng định lý Pytago vào tam giác vuông OBF và tam giác vuông ODB ta có:
BF=√OB2−OF2BF=OB2−OF2
BD=√OB2−OD2BD=OB2−OD2
Mà OF = OD nên BF = BD.
Tương tự áp dụng định lý Pytago vào tam giác vuông OEC và tam giác vuông ODC suy ra CE = CD
∆BAM có AB = BM nên ∆BAM là tam giác cân tại B ⇒ˆBAM=ˆBMA⇒BAM^=BMA^
Xét ∆BAM có BF = BD, BA = BM nên theo định lý Ta – lét ta có :
BFBA=BDBM⇒DF//AM⇒BFBA=BDBM⇒DF//AM⇒ DFAM là hình thang
Hình thang DFAM có ˆFAM=ˆAMDFAM^=AMD^ nên DFAM là hình thang cân
⇒{MF=ADAF=MD⇒{MF=ADAF=MD
∆ANC có AC = CN nên ∆ANC cân tại C⇒ˆCAN=ˆCNA⇒CAN^=CNA^
Xét ∆ANC có CE = CD, CA = CN nên theo định lý Ta – lét ta có :
CECA=CDCN⇒DE//AN⇒CECA=CDCN⇒DE//AN⇒ DEAN là hình thang
Hình thang DEAN có ˆCAN=ˆCNACAN^=CNA^ nên DEAN là hình thang cân
⇒{NE=ADAE=ND⇒{NE=ADAE=ND
⇒MF=NE⇒MF=NE
b) Xét ∆OEA và ∆ODN ta có :
⎧⎪⎨⎪⎩OE=ODˆOEA=ˆODNEA=DN{OE=ODOEA^=ODN^EA=DN⇒ΔOEA=ΔODN(c−g−c)⇒ON=OA⇒ΔOEA=ΔODN(c−g−c)⇒ON=OA
Xét ∆OAF và ∆OMD ta có :
⎧⎪⎨⎪⎩AF=MDˆOFA=ˆODMOF=OD{AF=MDOFA^=ODM^OF=OD⇒ΔOAF=ΔODM(c−g−c)⇒OA=OM⇒ΔOAF=ΔODM(c−g−c)⇒OA=OM
⇒OM=ON⇒OM=ON hay ∆MON cân tại O.
1 tháng 4 2017
Diện tích tam giác ANC = 1/3 diện tích tam giác AMC
vì hai tam giác này có chung chiều cao hạ từ đỉnh C mà đáy AN = 1/3 đáy AM
Diện tích tam giác AMC là :
36 x 3 = 108 ( cm2 )
Diện tích tam giác AMC = 2/3 diện tcihs tam giác ABC
vì 2 tam giác này có chung chiều cao hạ từ đỉnh A mà đáy MC = 2/3 đáy BC
a) Diện tích tam giác ABC là
108 : 2 x3 = 162 ( cm2 )
b) Nối B với N ta có diện tích tam giác BNM = 1/3 diện tích tam giác BNC
Vì hai tam giác này co chung chiều cao hạ từ đỉnh N mà đáy BM= 1/3 đáy BC
Diện tcihs tam giác ANC = 1/3 diện tcihs tam giác BNC
Diện tích tam giác ANC là :
36 x 3 = 108 ( cm2)
Diện tích tam giác ABN là :
162 - ( 108 + 36 ) = 18 ( cm2 )
Ta thấy hai tam giác ANC và BNC có chung cạnh NC mà diện tích tam giác ANC = 1/3 diện tích tam giác BNC
Nên chiều cao hạ từ đỉnh A = 1/3 chiều cao hạ từ đỉnh B ( AH = 1/3 BP)
Diện tích tam giác AKN = 1/3 diện h stam giác BNM
cạnh đáy KN mà chiều cao AH = 1/3 chiều cao BP
Ta thấy hai tam giác AKN và BKN có chung chiều cao hạ từ đỉnh N mà diện tích tam giác AKN = 1/3 diện tích tam giác
BKN nên đáy AK = 1/3 đáy BK vậy AK/BK = 1/3