chứng minh 3 điểm sau thẳng hàng
1) A(2;1) ; B(-1;2) ; C(\(\frac{-1}{2}\);3)
2) A(1;0) ;B(-4;1) ; C(-1;\(\frac{2}{5}\))
3) A(0;-1) ; B(2;5) ; C(-1;-4)
GIÚP MK VS MAI MK KTRA RÙI!!!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 6 2022
a: Gọi (d): y=ax+b là phương trình đường thẳng BC
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}-a+b=-1\\4a+b=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=1\end{matrix}\right.\)
Vậy: y=2x+1
b: Khi y=3 thì x+6=7
=>x=1
Thay x=1 và y=3 vào y=2x+1, ta được:
\(2\cdot1+1=3\)(đúng)
=>Ba đường đồng quy
c: \(\overrightarrow{AB}=\left(-3;-6\right)\)
\(\overrightarrow{BC}=\left(5;10\right)\)
Vì \(\dfrac{-3}{5}=\dfrac{-6}{10}\)
nên A,B,C thẳng hàng
CM
19 tháng 7 2019
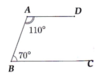
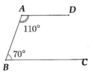
a) Ta có D A B ^ + A B C ^ = 180°.
Mà hai góc ở vị trí trong cùng phía.
Từ đó AD // BC (tính chất hai đường thẳng song song).
b) Cách 1:
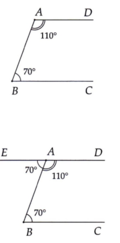
E A B ^ + B A D ^ = 70° + 110° = 180°
Cách 2: E A B ^ = A B C ^ = 70°
Mà hai góc ở vị trí so le trong nên AE// BC ( tính chất hai đường thẳng song song)
Lại có AD//BC ( chứng minh ý a)) nên Ad = AE.
Vậy E, A, D thẳng hàng
MT
4
26 tháng 5 2021
Gọi d: y = ax + b là đường thẳng đi qua hai điểm A, B.
Ta có \(\left\{{}\begin{matrix}2a+b=1\\-a+b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3a=-3\\b-a=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-1\\b=3\end{matrix}\right.\).
Do đó đường thẳng đi qua A, B là y = -x + 3.
Thay x = 3 vào ta được y = 0 nên C(3; 0) thuộc đường thẳng đó
9 tháng 12 2021
\(\overrightarrow{AB}=\left(-9;5\right)\)
\(\overrightarrow{AC}=\left(-\dfrac{9}{4};\dfrac{1}{2}\right)\)
Vì \(\overrightarrow{AB}=k\cdot\overrightarrow{AC}\) nên A,B,C thẳng hàng