 giúp với ạa
giúp với ạa
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Hướng dẫn:
Ta có:
\(x^2-xy+y^2=2x-3y-2\)
\(\Leftrightarrow2x^2-2xy+2y^2-4x+6y+4+9=9\)
\(\Leftrightarrow\left(x^2-2xy+y^2\right)+\left(x^2-4x+4\right)+\left(y^2+6y+9\right)=9\)
\(\Leftrightarrow\left(x-y\right)^2+\left(x-2\right)^2+\left(y+3\right)^2=9\)
Xét....
Đây là 1 cách nhưng làm hơi dài.
\(x^2-xy+y^2=2x-3y-2\\ \Leftrightarrow x^2-xy+y^2-2x+3y+2=0\left(1\right)\\ \Leftrightarrow x^2-x\left(y+2\right)+y^2+3y+2=0\)
Coi đây là pt bậc 2 ẩn x
Ta có: \(\Delta=\left[-\left(y+2\right)\right]^2-4\left(y^2+3y+2\right)=y^2+4y+4-4y^2-12y-8=-3y^2-8y-4\)
Để pt có nghiệm nguyên thì \(\Delta\ge0\Leftrightarrow-3y^2-8y-4\ge0\Leftrightarrow-2\le y\le-\dfrac{2}{3}\)
\(\Leftrightarrow y\in\left\{-2;-1\right\}\)
Thay y=-2 vào (1) ta có:
\(\left(1\right)\Leftrightarrow x^2-x.\left(-2\right)+\left(-2\right)^2-2x+3.\left(-2\right)+2=0\\ \Leftrightarrow x^2+2x+4-2x-6+2=0\\ \Leftrightarrow x^2=0\Leftrightarrow x=0\)
Thay y=-1 vào pt ta có:
\(\left(1\right)\Leftrightarrow x^2-x.\left(-1\right)+\left(-1\right)^2-2x+3.\left(-1\right)+2=0\\ \Leftrightarrow x^2+x+1-2x-3+2=0\\ \Leftrightarrow x^2-x=0\\ \Leftrightarrow x\left(x-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
Vậy \(\left(x,y\right)\in\left\{\left(0;-2\right);\left(0;-1\right);\left(1;-1\right)\right\}\)

a: 5 không là số nguyên tố
b: 4+x>=3
c: (căn 3+căn 12)^2 là số vô tỉ
d: Phương trình x^2+2023x=1 có nghiệm
e: 3^2+4^2<>5^2
f: căn 3*căn 27<>9
g: x=1 không là nghiệm của phương trình \(\dfrac{x^2-1}{x-1}=0\)
h: Tổng hai cạnh của một tam giác nhỏ hơn hoặc bằng cạnh còn lại



Bài 10:
Ta có:\(s=v_0.t+\dfrac{1}{2}.at^2\)
Quãng đường vật đi được trong 3s đầu là:
\(s_1=3v_0+a\dfrac{9}{2}=15\left(m\right)\)
Quãng đường vật đi được trong 3s tiếp theo là:
\(s_2=6v_0+18a-\left(3v_0+a\dfrac{9}{2}\right)=3v_0+a\dfrac{27}{2}=33\left(m\right)\)
Ta có hệ phương trình:
\(\left\{{}\begin{matrix}3v_0+a\dfrac{9}{2}=15\\3v_0+a\dfrac{27}{2}=33\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\left(m/s^2\right)\\v_0=2\left(m/s\right)\end{matrix}\right.\)
Bài 10:
Ta có:\(s=v_0.t+\dfrac{1}{2}.at^2\)
Quãng đường vật đi được trong 3s đầu là:
\(s_1=3v_0+a\dfrac{9}{2}=15\left(m\right)\)
Quãng đường vật đi được trong 3s tiếp theo là:
\(s_2=6v_0+18a-\left(3v_0+a\dfrac{9}{2}\right)=3v_0+a\dfrac{27}{2}=33\left(m\right)\)
Ta có hệ phương trình:
\(\left\{{}\begin{matrix}3v_0+a\dfrac{9}{2}=15\\3v_0+a\dfrac{27}{2}=33\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\left(m/s^2\right)\\v_0=2\left(m/s\right)\end{matrix}\right.\)
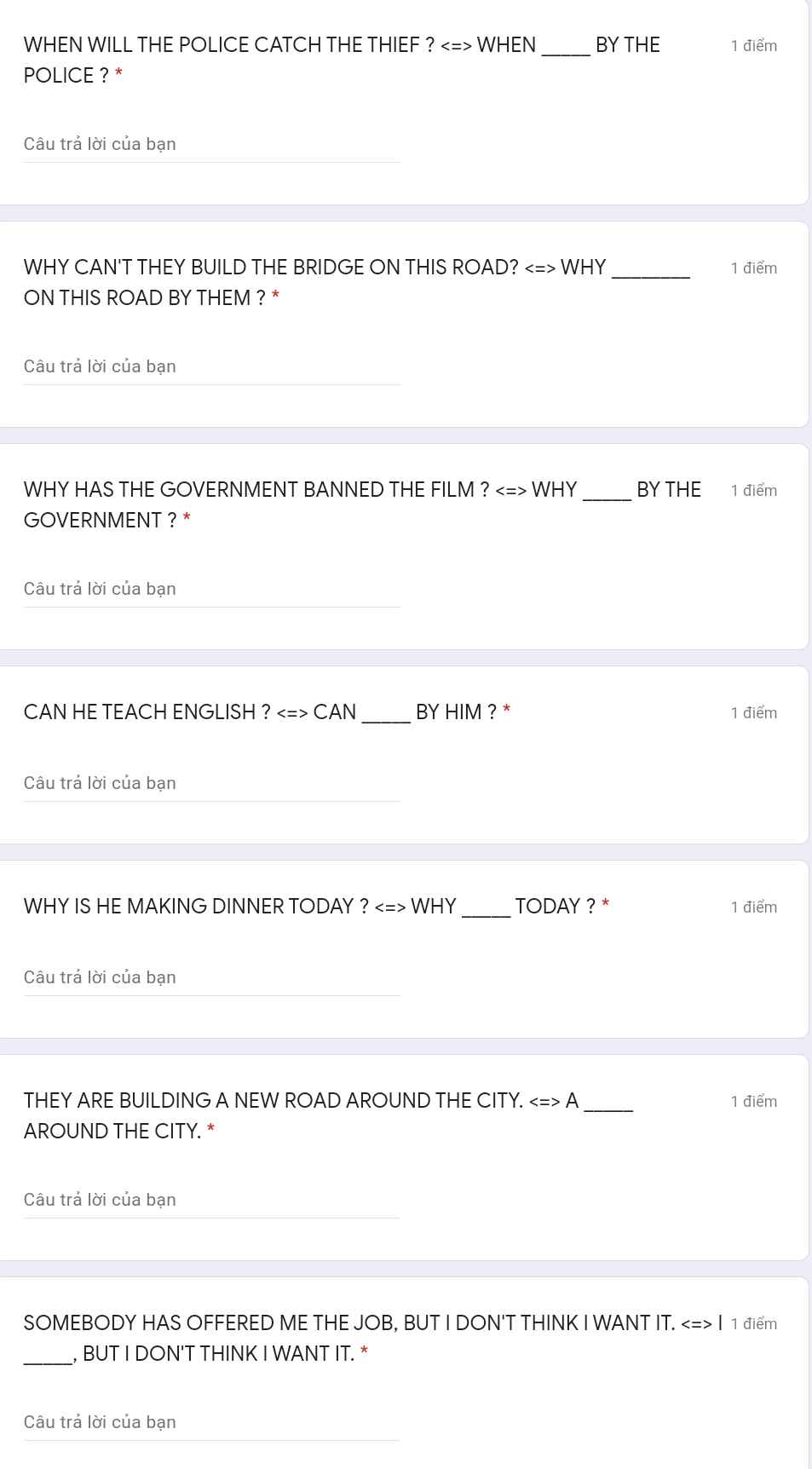 giúp em với ạa, bài này là bài tập không phải thi đâu ạa
giúp em với ạa, bài này là bài tập không phải thi đâu ạa
 giúp em với ạa
giúp em với ạa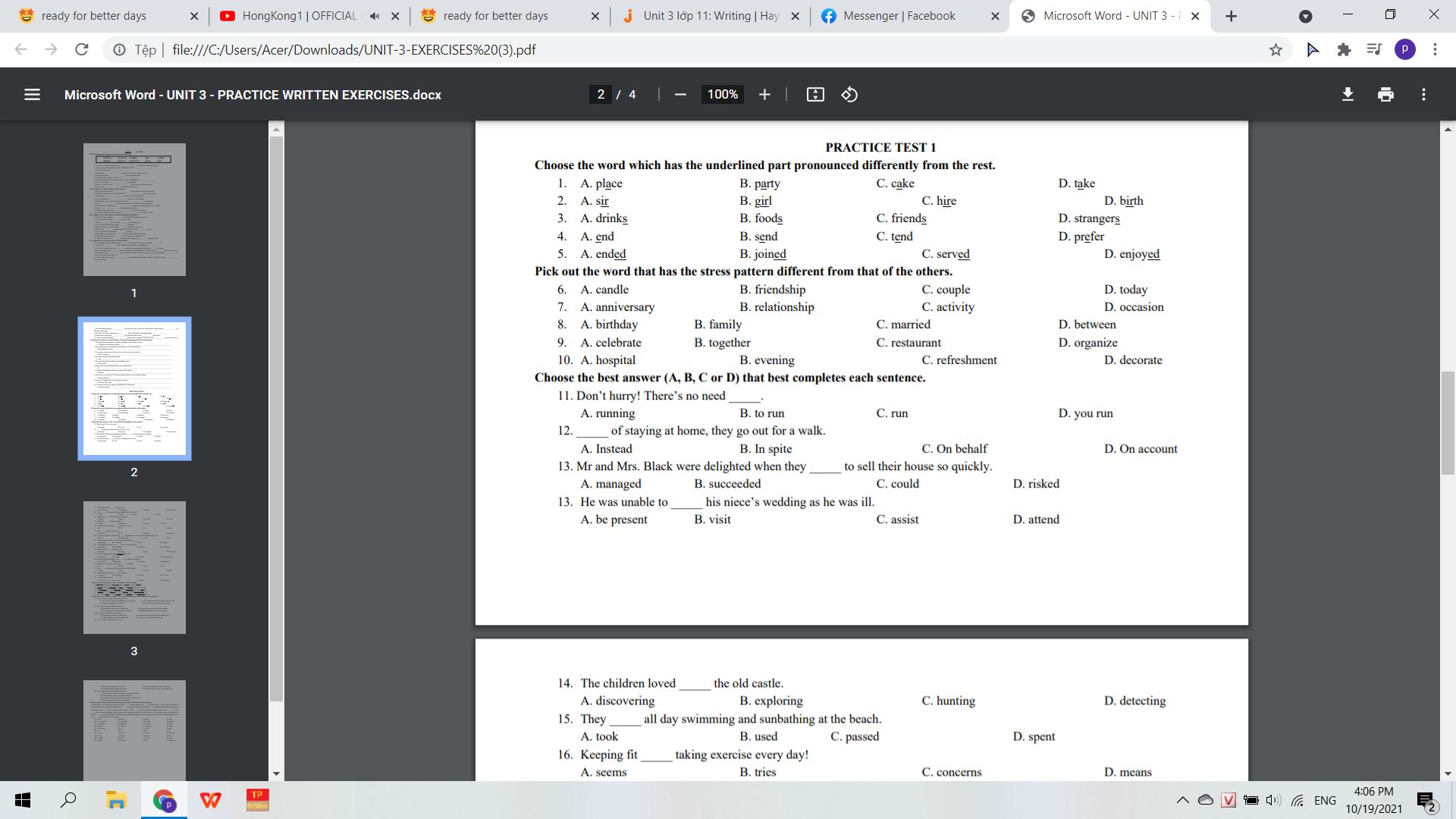
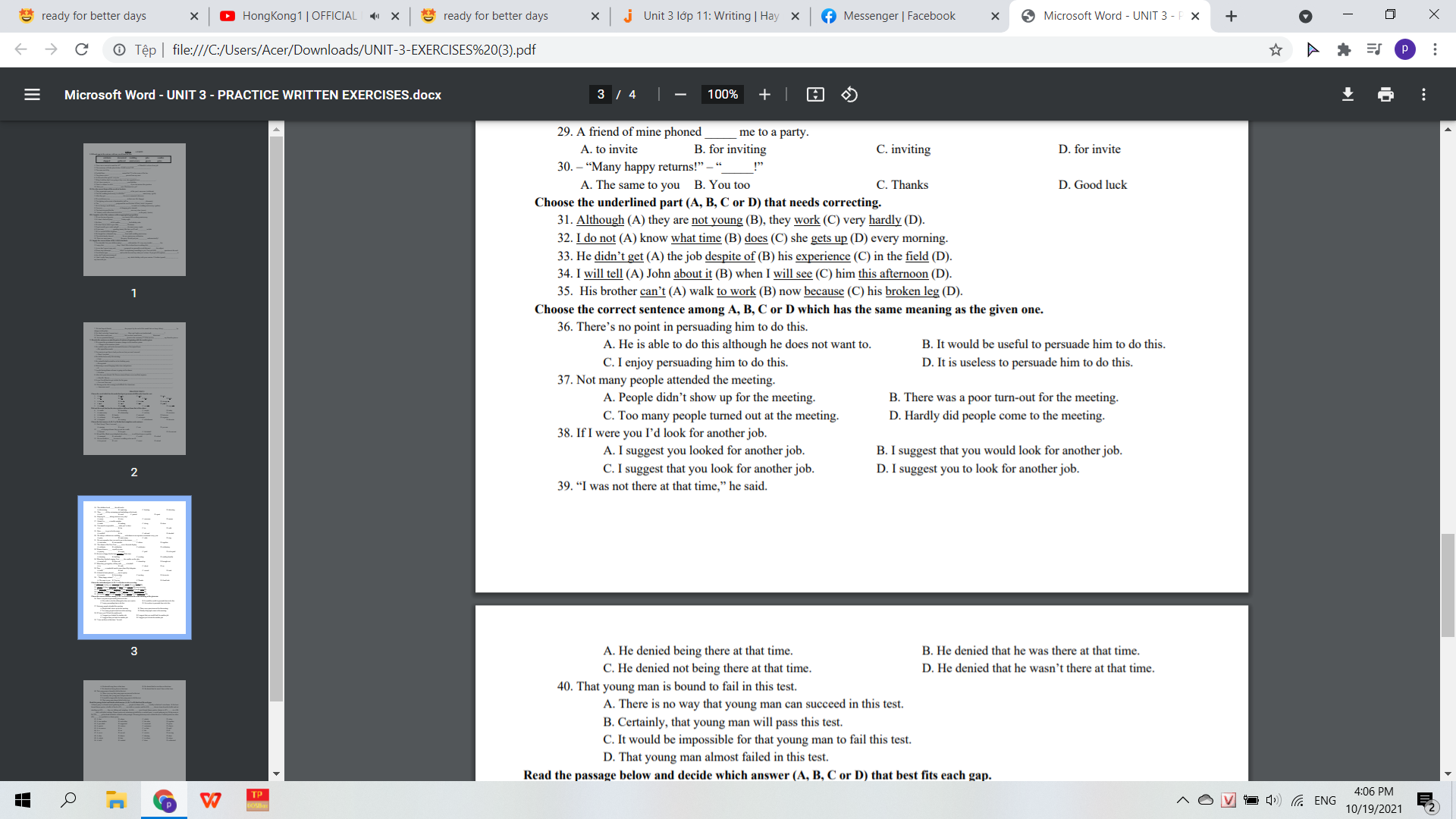

 giúp e với ạa
giúp e với ạa


Ta có: \(n_{SO_2}=\dfrac{6,72}{22,4}=0,3\left(mol\right)\)
a. PTHH:
Na2SO3 + H2SO4 ---> Na2SO4 + SO2 + H2O (1)
K2SO3 + H2SO4 ---> K2SO4 + SO2 + H2O (2)
Theo PT(1,2): \(n_{H_2SO_4}=n_{SO_2}=0,3\left(mol\right)\)
=> \(m_{H_2SO_4}=0,3.98=29,4\left(g\right)\)
b. Gọi x, y lần lượt là số mol của Na2SO3 và K2SO3
Theo PT(1,2):
=> x + y = 0,3
Theo đề, ta có: 126x + 158y = 44,2
=> x = 0,1, y = 0,2
Theo PT(1): \(n_{Na_2SO_4}=n_{Na_2SO_3}=0,1\left(mol\right)\)
=> \(m_{Na_2SO_4}=0,1.142=14,2\left(g\right)\)
Theo PT(2): \(n_{K_2SO_4}=n_{K_2SO_3}=0,2\left(mol\right)\)
=> \(m_{K_2SO_4}=0,2.164=34,8\left(g\right)\)
=> \(m_{sau.phản.ứng}=34,8+14,2=49\left(g\right)\)
Ta có: \(C_{\%_{H_2SO_4}}=\dfrac{0,3.98}{m_{dd_{H_2SO_4}}}.100\%=20\%\)
=> \(m_{dd_{H_2SO_4}}=147\left(g\right)\)
Ta có: \(m_{dd_{sau.phản.ứng}}=147+44,2=191,2\left(g\right)\)
=> \(C_{\%_{dd_{sau.phản.úng}}}=\dfrac{49}{191,2}.100\%=25,63\%\)
c. Đổi 500ml = 0,5 lít
=> \(n_{Ba\left(OH\right)_2}=1.0,5=0,5\left(mol\right)\)
Ta có: \(T=\dfrac{n_{SO_2}}{n_{Ba\left(OH\right)_2}}=\dfrac{0,3}{0,5}=0,6< 1\)
Vậy PTHH là: \(SO_2+Ba\left(OH\right)_2--->BaSO_3+H_2O\) (Ba(OH)2 dư.)
Theo PT: \(n_{BaSO_3}=n_{SO_2}=0,3\left(mol\right)\)
=> \(m_{BaSO_3}=0,3.217=65,1\left(g\right)\)
\(n_{SO_2}=\dfrac{6,72}{22,4}=0,3mol\)
\(Na_2SO_3+H_2SO_4\rightarrow Na_2SO_4+H_2O+SO_2\)
\(x\) \(x\)
\(K_2SO_3+H_2SO_4\rightarrow K_2SO_3+H_2O+SO_2\)
\(y\) \(y\)
Ta có: \(\left\{{}\begin{matrix}126x+158y=44,2\\x+y=0,3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=0,1\\y=0,2\end{matrix}\right.\)
a)\(\Rightarrow\Sigma n_{H_2SO_4}=0,1+0,2=0,3mol\)
\(\Rightarrow m_{H_2SO_4}=0,3\cdot98=29,4\left(g\right)\)
\(\Rightarrow m_{ddH_2SO_4}=\dfrac{29,4}{20}\cdot100=147\left(g\right)\)
b)