Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:
f(x+3) = a(x+3)2+ b(x+3) +c=ax2+ (6a+b) x+ 9a+ 3b+c
f(x+2) = a(x+2)2+ b(x+2) +c=ax2+ (4a+b) x+ 4a+ 2b+c
f (x+1) = a(x+1)2+ b(x+1) +c=ax2+ (2a+b) x+ 2a+ 2b+c
Suy ra: (x+ 3) -3f( x+ 2) +3f( x+ 1)= ax2+ bx+ c
Chọn D.

Lời giải:
Ta có: \(f(x)=ax^2+bx+c\)
\(\Rightarrow \left\{\begin{matrix} f(x+3)=a(x+3)^2+b(x+3)+c\\ f(x+2)=a(x+2)^2+b(x+2)+c\\ f(x+1)=a(x+1)^2+b(x+1)+c\\ f(x)=ax^2+bx+c\end{matrix}\right.\)
\(\Rightarrow f(x+3)-3f(x+2)+3f(x+1)-f(x)\)
\(=[f(x+3)-f(x)]-3[f(x+2)-f(x+1)]\)
Có:
\(f(x+3)-f(x)=a(x+3)^2+b(x+3)+c-[ax^2+bx+c]\)
\(=a[(x+3)^2-x^2]+b(x+3-x)\)
\(=3a(2x+3)+3b(1)\)
Và: \(f(x+2)-f(x+1)=a[(x+2)^2-(x+1)^2]+b[(x+2)-(x+1)]\)
\(=a(2x+3)+b\)
\(\Rightarrow 3[f(x+2)-f(x+1)]=3a(2x+3)+3b(2)\)
Từ (1)(2) suy ra:
\(f(x+3)-3f(x+2)+3f(x+1)-f(x)=3a(2x+3)+3b-[3a(2x+3)+3b]=0\)

Mình có nghĩ ra cách này mọi người xem giúp mình với
f(x) = \(ax^2+bx+c\)
Ta có f(0) = 2 => c = 2
Ta đặt Q(x) = \(ax^2+bx+c-2020\)
và G(x) = \(ax^2+bx+c+2021\)
f(x) - 2020 chia cho x - 1 hay Q(x) chia cho x - 1 được số dư
\(R_1\) = Q(1) = \(a.1^2+b.1+c-2020=a+b+c-2020\)
Mà Q(x) chia hết cho x-1 nên \(R_1\) = 0
hay \(a+b+c-2020=0\). Mà c = 2 => a + b = 2018 (1)
G(x) chia cho x + 1 số dư
\(R_2\) = G(-1) = \(a.\left(-1\right)^2+b.\left(-1\right)+c+2021=a-b+2+2021\)
Mà G(x) chia hết cho x + 1 nên \(R_2\)=0
hay \(a-b+2+2021=0\) => \(a-b=-2023\) (2)
Từ (1) và (2) suy ra: \(\left\{{}\begin{matrix}a+b=2018\\a-b=-2023\end{matrix}\right.\)
Vậy \(\left\{{}\begin{matrix}a=-\dfrac{5}{2}\\b=\dfrac{4041}{2}\end{matrix}\right.\)

Đặt \(g(x)=10x\).
Ta có \(g\left(1\right)=10=f\left(1\right);g\left(2\right)=20=f\left(2\right);g\left(3\right)=30=f\left(3\right)\).
Từ đó \(\left\{{}\begin{matrix}f\left(1\right)-g\left(1\right)=0\\f\left(2\right)-g\left(2\right)=0\\f\left(3\right)-g\left(3\right)=0\end{matrix}\right.\)
\(\Rightarrow f\left(x\right)-g\left(x\right)=Q\left(x\right).\left(x-1\right)\left(x-2\right)\left(x-3\right)\).
\(\Rightarrow f\left(x\right)=10x+Q\left(x\right)\left(x-1\right)\left(x-2\right)\left(x-3\right)\)
\(\Rightarrow f\left(8\right)+f\left(-4\right)=80+Q\left(x\right).7.6.5+\left(-40\right)+Q\left(x\right).\left(-5\right).\left(-6\right).\left(-7\right)=80-50=40\).
Đoạn cuối mình làm nhầm nhé.
Đáng lẽ phải cm Q(x) là đa thức dạng x + m, rồi biến đổi \(f\left(8\right)+f\left(-4\right)=80+Q\left(8\right).7.6.5+\left(-40\right)+Q\left(-4\right).\left(-5\right).\left(-6\right).\left(-7\right)=80-40+\left(m+8\right).7.6.5-\left(m-4\right).5.6.7=12.5.6.7+40=2560\).
Mình đánh vội nên chưa suy nghĩ kĩ.

Bài 1:
Cho $y=0$ thì: $f(x^3)=xf(x^2)$
Tương tự khi cho $x=0$
$\Rightarrow f(x^3-y^3)=xf(x^2)-yf(y^2)=f(x^3)-f(y^3)$
$\Rightarrow f(x-y)=f(x)-f(y)$ với mọi $x,y\in\mathbb{R}$
Cho $x=0$ thì $f(-y)=0-f(y)=-f(y)$
Cho $y\to -y$ thì: $f(x+y)=f(x)-f(-y)=f(x)--f(y)=f(x)+f(y)$ với mọi $x,y\in\mathbb{R}$
Đến đây ta có:
$f[(x+1)^3+(x-1)^3]=f(2x^3+6x)=f(2x^3)+f(6x)$
$=2f(x^3)+6f(x)=2xf(x^2)+6f(x)$
$f[(x+1)^3+(x-1)^3]=f[(x+1)^3-(1-x)^3]$
$=(x+1)f((x+1)^2)-(1-x)f((1-x)^2)$
$=(x+1)f(x^2+2x+1)+(x-1)f(x^2-2x+1)$
$=(x+1)[f(x^2)+2f(x)+f(1)]+(x-1)[f(x^2)-2f(x)+f(1)]$
$=2xf(x^2)+4f(x)+2xf(1)$
Do đó:
$2xf(x^2)+6f(x)=2xf(x^2)+4f(x)+2xf(1)$
$2f(x)=2xf(1)$
$f(x)=xf(1)=ax$ với $a=f(1)$

\(f\left(x^5+y^5+y\right)=x^3f\left(x^2\right)+y^3f\left(y^2\right)+f\left(y\right)\)
Sửa lại đề câu 2 !!
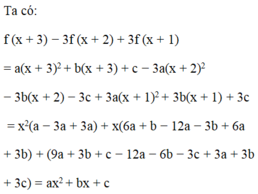
\(f\left(x+3\right)-3f\left(x+2\right)+3f\left(x+1\right)\)
\(=a\left(x+3\right)^2+b\left(x+3\right)+c-3\left[a\left(x+2\right)^2+b\left(x+2\right)+c\right]+3\left[a\left(x+1\right)^2+b\left(x+1\right)+c\right]\)
\(=3a\left(x+1\right)^2+a\left(x+3\right)^2-3a\left(x+2\right)^2+bx+c\)
\(=ax^2+bx+c\)