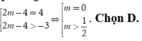Tìm nghiệm nguyên của phương trình : x4 – y2 + 2x2 + y + 6 =0
Giúp mik với minh xin cảm ơn!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét hàm số
y = x 4 - 2 x 2 - 1 ⇒ y ' = 4 x 3 - 4 x = 4 x x - 1 x + 1 = 0 ⇔ x = 0 x = ± 1
Ta có BBT như sau:
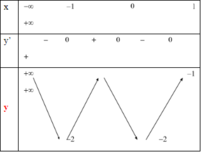
PT x 4 - 2 x 2 - 1 = log 4 m có 6 nghiệm
⇔ 1 < log 4 m < 2 ⇔ 4 < m < 16
Vậy m có 11 giá trị nguyên.
Đáp án cần chọn là B

Ta có x4 + x2 + 1 = y2
Lại có x4 + 2x2 + 1 ≥ x4 + x2 + 1 hay (x2 + 1)2 ≥ x4 + x2 + 1
=> (x2 + 1)2 ≥ y2 (1)
Lại có x4 + x2 + 1 > x4 => y2 > x4 (2)
Từ (1) và (2), ta có x4 < y2 ≤ (x2 + 1)2
<=> y2 = (x2 + 1)2 = x4 + 2x2 + 1
Mà x4 + x2 + 1 = y2 => x4 + 2x2 + 1 = x4 + x2 + 1
<=> x2 = 0 <=> x = 0
Thay vào, ta có 1 = y2 <=> y ∈ {-1,1}
Vậy ...



Từ đồ thị hàm số, suy ra phương trình x 4 - 2 x 2 - 3 = 2 m - 4 có hai nghiệm phân biệt khi và chỉ khi