Question

[Nguyễn Thị Hồng Huế]

Tóm tắt và giải bài sau

Một người đi xe đạp từ A đến B với vận tốc v₁= 12km/h . Nếu người đó tăng vận tốc lên 3km/ h thì đến nơi sớm hơn 1h.

Tìm quãng đường AB và thời gian dự định đi từ A đến B.

Ban đầu người đó đi với vận tốc v_{1=12km/h được một quãng đường s1 thì xe bị hư phải sữa chữa mất 15ph . Do đó quãng đường còn lại người ấy đi với vận tốc v2 =15km/h thì đến sớm hơn dự định 30ph . Tìm quãng đường s1}

Answer 1

[❤ ~~ Yến ~~ ❤]

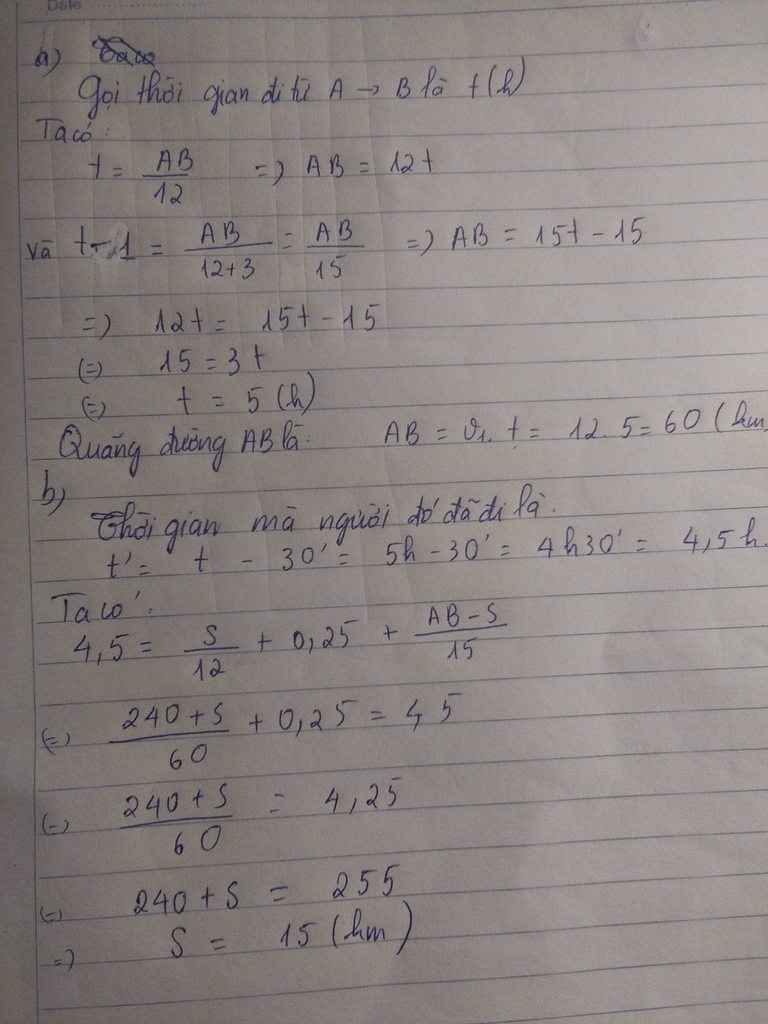
Giải:

Tóm tắt:

v₁ =12km/h

t =15' = \(\frac{1}{4}h\)

v₂ =15lm/h

* t=?

*s₁ = ?

Giải

* Gọi quãng đường AB là s (km)

Ta có: s = v₁ . t

s = (v₁ + 3)(t - 1)

⇔ v₁t = (v₁ + 3)(t - 1)

⇔ 12.t = (12 + 3)(t -1)

⇔ 12t = 15t - 15

⇒ t = 5h

* Thời gian đi hết quãng đường \(\frac{s_1}{t_1'}=\frac{s_1}{v_1}\)

Thời gian sửa xe:t = 15' = \(\frac{1}{4}h\)

Thời gian đi quãng đường còn lại:t₂' = \(\frac{s-s_1}{v_2}\)

Theo bài ta có: \(t_1-\left(t_1'+\frac{1}{4}+t_2'\right)=30'=\frac{1}{2}h\)

\(t_1-\left(\frac{s_1}{v_1}+\frac{1}{4}+\frac{s-s_1}{v_2}\right)=\frac{1}{2}\)

⇔ \(\frac{s}{v_1}-\frac{s}{v_2}-s_1\left(\frac{1}{v_1}-\frac{1}{v_2}\right)=\frac{1}{2}+\frac{1}{4}=\frac{3}{4}\)

⇔ \(s_1\left(\frac{1}{v_1}-\frac{1}{v_2}\right)=1-\frac{1}{3}=\frac{1}{4}\)

⇔ \(s_1=\frac{1}{4}.\frac{v_1v_2}{v_2-v_1}=\frac{1}{4}.\frac{12.15}{15-12}=15km\)