Cho hai vecto a và b. Trong trường hợp nào thì đẳng thức sau là đúng:
/ vecto a+ vecto b/= / vecto a - vecto b/
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bình phương 2 vế:
\(\Leftrightarrow\overrightarrow{a}^2+\overrightarrow{b^2}+2\overrightarrow{a}.\overrightarrow{b}=\overrightarrow{a}^2+\overrightarrow{b}^2-2\overrightarrow{a}.\overrightarrow{b}\)
\(\Leftrightarrow\overrightarrow{a}.\overrightarrow{b}=0\)
\(\Leftrightarrow\overrightarrow{a}\perp\overrightarrow{b}\)
Vậy đẳng thức xảy ra khi 2 vecto có phương vuông góc nhau

Phương án A và C sai vì có thể xảy ra trường hợp như hình vẽ sau
Giả sử phương án B cũng sai, tức là ba vecto n → , a → v à b → đồng phẳng. Khi đó vì n→ ⊥ a→ và n→ ⊥ b→ nên giá của a → v à b → song song. Điều này mẫu thuẫn với giả thiết hai vecto a → v à b → không cùng phương. Vì vậy phương án B đúng.
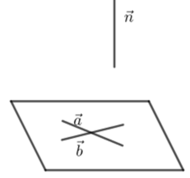
Đáp án B

\(\cos\left(\overrightarrow{a},\overrightarrow{b}\right)=\dfrac{\left(-1\right)\cdot2+1\cdot0}{\sqrt{\left(-1\right)^2+1^2}+\sqrt{2^2+0^2}}=-2+\sqrt{2}\)
\(\Leftrightarrow\left(\overrightarrow{a},\overrightarrow{b}\right)=125^0\)
Đẳng thức đúng khi và chỉ khi \(\overrightarrow{a}.\overrightarrow{b}=0\) hay \(\overrightarrow{a}\perp\overrightarrow{b}\) hoặc 1 trong 2 vecto là vecto - không