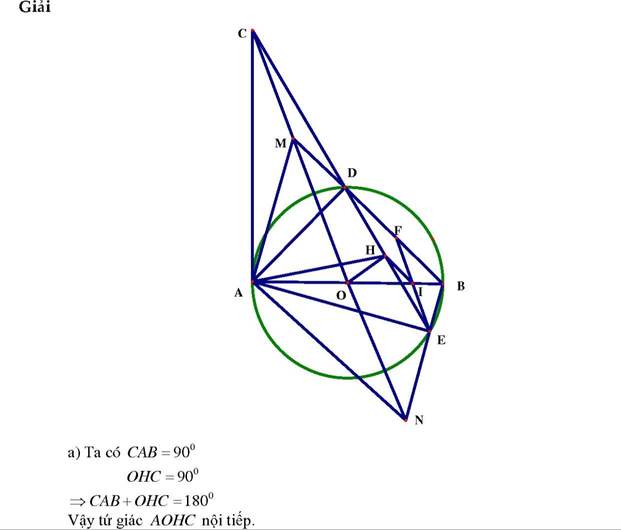
Cho đường tròn (O) và đường thẳng d không giao nhau. Vẽ OH vuông góc với d tại H, vẽ cát tuyến HAB với đường tròn ( A nằm giữa H và B). Vẽ hai tiếp tuyến Ax, By với đường tròn cắt d theo thứ tự tại m và E.
a) Chứng minh 4 điểm A, O, M, H cùng thuộc một đường tròn;
b) Chứng minh HM = HE.



a) Ta có góc OAM = góc OHM = 900
suy ra OAMH là tứ giác nội tiếp
b) CM tương tự ta cũng có tứ giác OHEB nội tiếp
góc OMA = góc OHA ( cùng chắn cung OA)(1)
góc OHA = góc OEB ( cùng chắn cung OB)(2)
Từ (1) và (2) suy ra góc OMA = gocs OEB
Suy ra: tam giác OMA = tam giác OEB (gcg)
nên OM = OE
tam giác OME cân có OH là đường cao đồng thời là trung tuyến
=> HM= HE