Cho tam giác ABC có góc B=60 độ. Hãy chứng minh rằng:
\(AC^2=AB^2+BC^2-AB.BC\)
Chú ý : KHÔNG SỬ DỤNG ĐỊNH LÝ HÀM COS.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


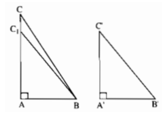
Do AC > A'C' nên lấy được điểm C1 trên cạnh AC sao cho AC1=A′C′. Ta có tam giác vuông ABC1 bằng tam giác vuông A'B'C', suy ra B′C′=BC1. Mặt khác hai đường xiên BC và BC1 kẻ từ B đến đường thẳng AC lần lượt có hình chiếu trên AC là AC và AC1. Vì AC > AC1 nên BC > BC1. Suy ra BC > B'C'.

Dùng phản chứng:
- Giả sử AC < A'C'. Khi đó theo chứng minh câu a) ta có BC < B'C'. Điều này không đúng với giả thiết BC > B'C'.
Giả sử AC = A'C'. Khi đó ta có ΔABC = ΔA'B'C' (c.g.c). Suy ra BC = B'C'.
Điều này cũng không đúng với giả thiết BC > B'C'. Vậy ta phải có AC > A'C'.
(Nếu sử dụng định lý Pytago thì có thể giải bài toán sau)
Trong tam giác vuông ABC có BC 2= AB 2+ AC 2 (1)
Trong tam giác vuông A'B'C' có B'C' 2= A'B' 2+ A'C' 2 (2)
Theo giả thiết AB = A'B' nên từ (1) và (2) ta có:
- Nếu AC > A'C' thì AC 2 > A'C' 2, suy ra BC 2 > B'C' 2 hay BC > B'C'
- Nếu BC > B'C' thì BC 2 > B'C' 2, suy ra AC 2 > A'C' 2 hay AC > A'C'.

kẻ BH _|_ BC tại H
xét tam giác ABH vuông tại H
=> góc ABH + góc BAC = 90 (đl)
góc BAC = 60 (gt)
=> góc ABH = 30 ; xét tam giác ABH vuông tại H
=> AH = BA/2 (định lí)
=> AB = 2AH (1)
xét tam giác ABH vuông tại H
=> AB^2 = AH^2 + BH^2 (đl pytago)
=> BH^2 = AB^2 - AH^2 (2)
xét tam giác BHC vuông tại H
=> BC^2 = HC^2 + BH^2 (đl Pytago)
HC = AC - AH
=> BC^2 = (AC - AH)^2 + BH^2
=> BC^2 = AC^2 - 2AC.AH + AH^2 + BH^2 và (1)(2)
=> BC^2 = AC^2 - AB.AC + AH^2 + AB^2 - AH^2
=> BC^2 = AB^2 + AC^2 - AB.AC


a: Do AC > A'C' nên lấy được điểm C1 trên cạnh AC sao cho AC1=A′C′.
Ta có ΔABC1=ΔA'B'C'
Suy ra B′C′=BC1
Mặt khác hai đường xiên BC và BC1 kẻ từ B đến đường thẳng AC lần lượt có hình chiếu trên AC là AC và AC1.
Vì AC > AC1 nên BC > BC1.
Suy ra BC > B'C'.
b:
-Giả sử AC<A'C'.
Khi đó theo chứng minh câu a) ta có BC < B'C'. Điều này không đúng với giả thiết BC > B'C'.
Giả sử AC=A'C'. Khi đó ta có ΔABC=ΔA'B'C' (c.g.c).
Suy ra BC=B'C'.
Điều này cũng không đúng với giả thiết BC>B'C'. Vậy ta phải có AC>A'C'.
Kẻ CH\(\perp\)AB (H\(\in\)AB)
\(\Delta\)BCH vuông tại H có ^B = 600 nên BH = 1/2BC (cạnh đối diện với góc 300 trong tam giác vuông bằng nửa cạnh huyền) hay BC = 2BH
Áp dụng định lý Py-ta-go vào các tam giác AHC và HBC cùng vuông tại H, ta được: AC2 = AH2 + HC2 = (AB - HB)2 + HC2 = AB2 - 2.AB.HB + HB2 + HC2 = AB2 - AB.BC + BC2 (do theo chứng minh trên thì BC = 2BH)
Vậy AC2 = AB2 + BC2 - AB.BC (đpcm)