cho đường thẳng d1 và d2 song song lần lượt có pt \(x-2y+1=0\) và \(x-2y+4=0\). phép vị tự tâm \(I\left(2;1\right)\) tỉ số k biến đg thg d1 thành d2. tính gtri k?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Do 4 đỉnh hình vuông nằm trên 2 đường thẳng song song nên độ dài cạnh hình vuông chính là khoảng cách giữa hai đường thẳng song song
Ta có: d2: - x + 2y + 10= 0 hay 2x – 4y – 20 = 0
Khoảng cách hai đường thẳng là: d ( d 1 ; d 2 ) = 1 − ( − 20 ) 2 2 + ( − 4 ) 2 = 21 20
Diện tích hình vuông cần tính là: S = 21 20 2 = 441 20
ĐÁP ÁN D.

Giao điểm A của d1 và d2 là nghiệm:
\(\left\{{}\begin{matrix}x+2y+1=0\\x+y-5=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=11\\y=-6\end{matrix}\right.\)
\(\Delta\) song song d3 nên nhận (2;3) là 1 vtpt, nên có pt:
\(2\left(x-11\right)+3\left(y+6\right)=0\Leftrightarrow2x+3y-4=0\)

Với d1: 4x – 2y + 6 = 0 có vecto pháp tuyến là: n1→(4;-2)
và d2: x – 3y + 1 = 0 có vecto pháp tuyến là: n2→(1;-3) ; ta có :
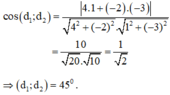

Hai đường thẳng song song khi m 3 = 2 − 4 ≠ − 3 2 n ê n m = − 3 2
Chọn đáp án C.

1.
Trục Ox có pt \(y=0\) nên đường song song với nó là \(y=4\)
2.
\(\overrightarrow{MI}=\left(1;-2\right)\)
Đường thẳng tiếp xúc với đường tròn tâm I tại M đi qua M và vuông góc MI nên nhận \(\overrightarrow{MI}\) là 1 vtpt
Phương trình:
\(1\left(x-1\right)-2\left(y-3\right)=0\Leftrightarrow x-2y+5=0\)
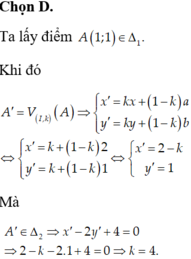
Gọi \(A\left(-1;0\right)\) là 1 điểm thuộc d1
Gọi \(A'\left(a;b\right)\) là ảnh của A qua phép vị tự tâm I tỉ số k
\(\Rightarrow\left\{{}\begin{matrix}a-2=k\left(-1-2\right)\\b-1=k\left(0-1\right)\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=-3k+2\\b=-k+1\end{matrix}\right.\)
Do A' thuộc d2 nên thay vào pt d2 ta được:
\(-3k+2-2\left(-k+1\right)+4=0\)
\(\Leftrightarrow k=4\)