cho tam giác ABC vuông tại A có cạnh AB=3, AC=4. phép vị tự tâm I tỉ số \(k=-\sqrt{2}\) biến tam giác ABC thành A'B'C'. tính diện tích tam giác A'B'C'
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
29 tháng 11 2017
Đáp án A
B = V A ; k ( M ) và 2 M A → = A B →
C = V A ; k ( N ) và 2 N A → = A C →
=>k = 2
CM
9 tháng 8 2018
Đáp án B
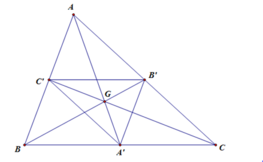
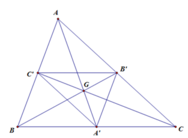
G A → = − 2 G A ' → ⇒ V G , − 2 A ' = A G B → = − 2 G B ' → ⇒ V G , − 2 B ' = B G C → = − 2 G C ' → ⇒ V G , − 2 C ' = C ⇒ V G , − 2 Δ A ' B ' C ' = Δ A B C
CM
7 tháng 4 2019
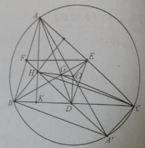
Phép vị tự tâm G tỉ số -1/2 biến A thành D; biến B thành E; biến C thành F ⇒ biến tam giác ABC thành tam giác DEF.
Đáp án B
CM
6 tháng 9 2017
Đáp án B
A’ = V G ; k ( A ) => − 2 G A ' → = G A → =>Tỉ số vị tự k = – 2
CM
1 tháng 11 2017
Đáp án B
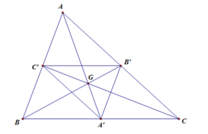
G A → = − 2 G A ' → ⇒ V G , − 2 A ' = A G B → = − 2 G B ' → ⇒ V G , − 2 B ' = B G C → = − 2 G C ' → ⇒ V G , − 2 C ' = C ⇒ V G , − 2 Δ A ' B ' C ' = Δ A B C
CM
12 tháng 7 2017
Gọi A’ là điểm đối xứng với A qua tâm O.
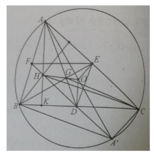
chứng minh BHCA’ là hình bình hành, suy ra H, A', D thẳng hàng và DO là đường trung bình của tam giác AHA’ ⇒ D O → = - 1 / 2 A H → ⇒ phép vị tự tâm G tỉ số -1/2 biến A H → thành DO → .
Đáp án B
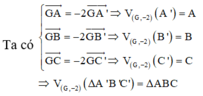
\(S_{ABC}=\frac{1}{2}AB.AC=6\)
Phép vị tự biến tam giác ABC thành A'B'C' với tỉ số đồng dạng \(\left|k\right|=\sqrt{2}\)
Do đó \(S_{A'B'C'}=k^2.S_{ABC}=12\)