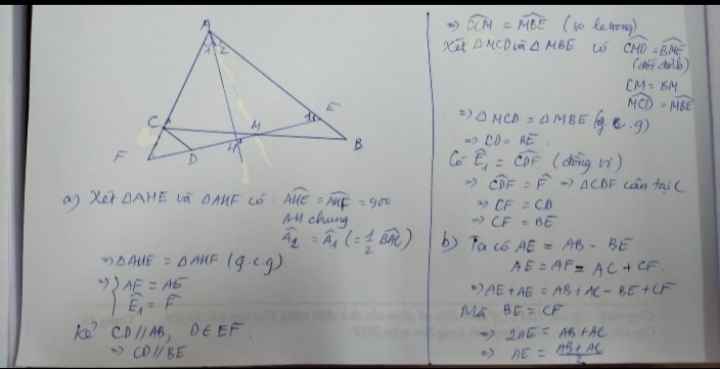
Bài 1: Cho tam giác ABC có AB>AC. Từ trung điểm M của BC vẽ 1 đường thẳng vuông góc với tia phân giác \(\widehat{A}\)cắt tia phân giác tại H , cắt AB, AC lần lượt tại các điểm E, F. Chứng Minh:
a, BE=CF
b, AE=\(\frac{AB+AC}{2}\), BE=\(\frac{AB-AC}{2}\) c,\(\widehat{BME}\)=\(\frac{\widehat{ACB-\widehat{B}}}{2}\)
Bài 2: Cho tam giác ABC, điểm S nằm ngoài tam giác ABC và thuộc nửa mặt phẳng bờ là đường thẳng AC không chứa B . Trên các tia đối của SA,SB,SC theo thứ tự lấy điểm D,E,F sao cho SA=SD, SE=SB, SF=SC. CM
a, Tam giác ABC= tam giác DEF
b, Gọi M là điểm bất kỳ thuộc đoạn thẳng BC. Trên tia đối của tia SM lấy N sao cho SM=SN. CM 3 điểm E,F,N thẳng hàng