Cho tam giác ABC vuông tại A. Kẻ đường phân giác BD, kẻ DE vuông góc BC
a) Chứng minh rằng: BD là trung trực của AE và AD<DC.
b) Tia ED cắt BA tại F. Chứng minh BD vuông góc CF và AE song song CF
c) Tia BD cắt CF tại G. chứng minh rằng D cách đều ba cạnh của tam giác AEG
d) lấy M và N tương ứng di động trên BF và bc sao cho BM + BN = BC. Chứng minh rằng trung điểm I của MN luôn nằm trên một đường thẳng cố...
Đọc tiếp
Cho tam giác ABC vuông tại A. Kẻ đường phân giác BD, kẻ DE vuông góc BC
a) Chứng minh rằng: BD là trung trực của AE và AD<DC.
b) Tia ED cắt BA tại F. Chứng minh BD vuông góc CF và AE song song CF
c) Tia BD cắt CF tại G. chứng minh rằng D cách đều ba cạnh của tam giác AEG
d) lấy M và N tương ứng di động trên BF và bc sao cho BM + BN = BC. Chứng minh rằng trung điểm I của MN luôn nằm trên một đường thẳng cố định
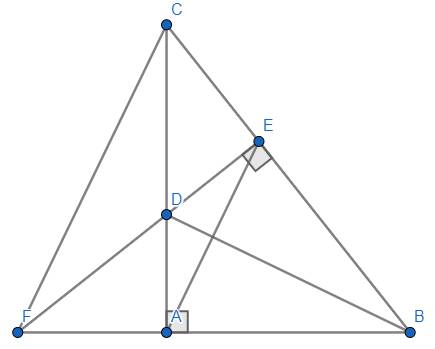
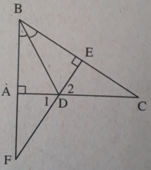
a) Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
Do đó: ΔABD=ΔEBD(cạnh huyền-góc nhọn)
⇔DA=DE(hai cạnh tương ứng)
nên D nằm trên đường trung trực của AE(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: ΔABD=ΔEBD(cmt)
⇒BA=BE(hai cạnh tương ứng)
nên B nằm trên đường trung trực của AE(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra BD là đường trung trực của AE(đpcm)
Xét ΔDEC vuông tại E có DC là cạnh đối diện với \(\widehat{DEC}=90^0\)
nên DC là cạnh huyền của ΔDEC vuông tại E
⇔DC là cạnh lớn nhất trong ΔDEC(Trong tam giác vuông, cạnh huyền là cạnh lớn nhất)
hay DE<DC(3)
mà DA=DE(cmt)(4)
nên từ (3) và (4) suy ra AD<DC
b) Xét ΔADF vuông tại A và ΔEDC vuông tại E có
DA=DE(cmt)
\(\widehat{ADF}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔADF=ΔEDC(cạnh góc vuông-góc nhọn kề)
⇒DF=DC(hai cạnh tương ứng)
hay D nằm trên đường trung trực của CF(Tính chất đường trung trực của một đoạn thẳng)(5)
Ta có: ΔADF=ΔEDC(cmt)
⇒AF=EC(hai cạnh tương ứng)
Ta có: BA+AF=BF(A nằm giữa hai điểm B và F)
BE+EC=BC(E nằm giữa hai điểm B và C)
mà BA=BE(cmt)
và AF=EC(cmt)
nên BF=BC
hay B nằm trên đường trung trực của CF(Tính chất đường trung trực của một đoạn thẳng)(6)
Từ (5) và (6) suy ra BD là đường trung trực của CF
hay BD⊥CF(đpcm)
Ta có: BD là đường trung trực của AE(cmt)
⇔BD⊥AE
Ta có: BD⊥AE(cmt)
BD⊥CF(cmt)
Do đó: AE//CF(Định lí 1 từ vuông góc tới song song)
cảm ơn bạn rất nhiều nhưng phiền bạn có thể trả lời nốt 2 câu còn lại ko