Tìm m để hàm số
y= \(-1\over3\)x3+(m+1)x2+(m+3)x đồng biến trên (0;3)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn B
y ' = x 2 - 2 x + ( m - 1 ) .
Hàm số đồng biến trên R ⇔ y' ≥ 0 ∀x ∈ R
⇒ Δ = ( - 1 ) 2 - ( m - 1 ) = - m + 2 ≤ 0 ⇔ m > 2

Đáp án: D.
Hàm số đồng biến trên tập xác định R khi và chỉ khi
y' = 3 x 2 - 4mx + 12 ≥ 0, ∀ x ⇔ ∆ ' = 4m2 - 36 ≤ 0 ⇔ -3 ≤ m ≤ 3.

Đáp án: D.
Hàm số đồng biến trên tập xác định R khi và chỉ khi
y' = 3 x 2 - 4mx + 12 ≥ 0, ∀x ⇔ Δ' = 4 m 2 - 36 ≤ 0 ⇔ -3 ≤ m ≤ 3.

Đáp án A
Phương pháp giải:
Dựa vào điều kiện để hàm số đồng biến hoặc nghịch biến trên khoảng xác định
Lời giải:
Ta có
y
=
x
3
-
3
m
x
2
+
3
(
2
m
-
1
)
x
+
1
![]() R
R
Hàm số đồng biến trên R ![]() R
R ![]() R
R
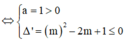
![]()
\(y'=f\left(x\right)=-x^2+2\left(m+1\right)x+m+3\)
Hàm đã cho đồng biến trên \(\left(0;3\right)\) khi và chỉ khi \(y'=0\) có 2 nghiệm pb thỏa mãn \(x_1\le0< 3\le x_2\)
\(\Leftrightarrow\left\{{}\begin{matrix}f\left(0\right)\ge0\\f\left(3\right)\ge0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m+3\ge0\\7m\ge0\end{matrix}\right.\) \(\Rightarrow m\ge0\)