Anh chị giúp e câu toán 9 với ạ .Ngày mai e kt giữa kì r .Em cảm ơn rất nhiều luôn ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TN
2
Những câu hỏi liên quan
TN
1
28 tháng 10 2021
\(P=\dfrac{x+2\sqrt{x}+x-2\sqrt{x}}{x-4}.\dfrac{x-4}{-2\sqrt{x}}=\dfrac{2x}{-2\sqrt{x}}=-\sqrt{x}\)
\(P=-\sqrt{x}=-\sqrt{4}=-2\left(đpcm\right)\)
16 tháng 11 2021
Bài 2:
\(\dfrac{1}{2}:\dfrac{5}{4}=x:\dfrac{10}{3}\Leftrightarrow\dfrac{1}{2}.\dfrac{4}{5}=\dfrac{3}{10}x\Leftrightarrow\dfrac{3}{10}x=\dfrac{2}{5}\Leftrightarrow x=\dfrac{2}{5}:\dfrac{3}{10}=\dfrac{4}{3}\)
Bài 3:
Áp dụng t/c dtsbn:
\(\dfrac{x}{4}=\dfrac{y}{12}=\dfrac{x+y}{4+12}=\dfrac{48}{16}=3\)
\(\Rightarrow\left\{{}\begin{matrix}x=3.4=12\\y=3.12=36\end{matrix}\right.\)
TN
1
28 tháng 10 2021
\(a,P=\dfrac{3\sqrt{a}-3}{\sqrt{a}\left(\sqrt{a}+1\right)}\cdot\dfrac{\left(\sqrt{a}+1\right)^2}{\sqrt{a}-1}\left(a\ge0;a\ne1\right)\\ P=\dfrac{3\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}{\sqrt{a}\left(\sqrt{a}-1\right)}=\dfrac{3\left(\sqrt{a}+1\right)}{\sqrt{a}}\\ b,a=4\Leftrightarrow\sqrt{a}=2\\ \Leftrightarrow P=\dfrac{3\left(2+1\right)}{2}=\dfrac{9}{2}\)
JP
1
29 tháng 7 2023
Gọi xy là tiếp tuyến tại A của (O)
=>góc xAC=góc ABC
xy//DE
=>góc xAE=góc AED
=>góc AED=góc ABC
Xét ΔAED và ΔABC có
góc AED=góc ABC
góc EAD chung
=>ΔAED đồng dạng với ΔABC
=>AE/AB=AD/AC
=>AE*AC=AB*AD
JP
1
23 tháng 3 2022
Câu 1:
Ta có 2x - y = 8 => 2x - y + 9 = 17
Mà 3x + y = 17 => 2x - y + 9 = 3x + y
<=> 9 - y = x + y <=> 9 = x + 2y <=> x = 9 - 2y
Mà 2x - y = 8 => 18 - 4y - y = 8 => 18 - 5y = 8 => y = 2 => x = 5
JP
1
MA
2
15 tháng 11 2021
\(d,=\dfrac{3y}{5x\left(x-y\right)}\\ e,=\dfrac{5x\left(x+2\right)\left(2-x\right)}{4\left(x-2\right)\left(x+2\right)}=\dfrac{-5x}{4}\\ f,=\dfrac{3\left(x-6\right)\left(x+6\right)}{2\left(x+5\right)\left(6-x\right)}=\dfrac{-3\left(x+6\right)}{2\left(x+5\right)}\\ g,=\dfrac{3xy\left(x-3y\right)\left(x+3y\right)}{2x^2y^2\left(x-3y\right)}=\dfrac{3\left(x+3y\right)}{2xy}\\ h,=\dfrac{45x^2y\left(x-y\right)\left(x+y\right)}{10xy\left(y-x\right)}=\dfrac{-9x\left(x+y\right)}{2}\\ i,=\dfrac{12\left(a-b\right)\left(a+b\right)\left(a^2+ab+b^2\right)}{3\left(a+b\right)\left(a-b\right)^2}=\dfrac{4\left(a^2+ab+b^2\right)}{a-b}\)
15 tháng 11 2021
e: \(=\dfrac{5\left(x+2\right)}{4\left(x-2\right)}\cdot\dfrac{-2\left(x-2\right)}{x+2}=\dfrac{-10}{4}=-\dfrac{5}{2}\)
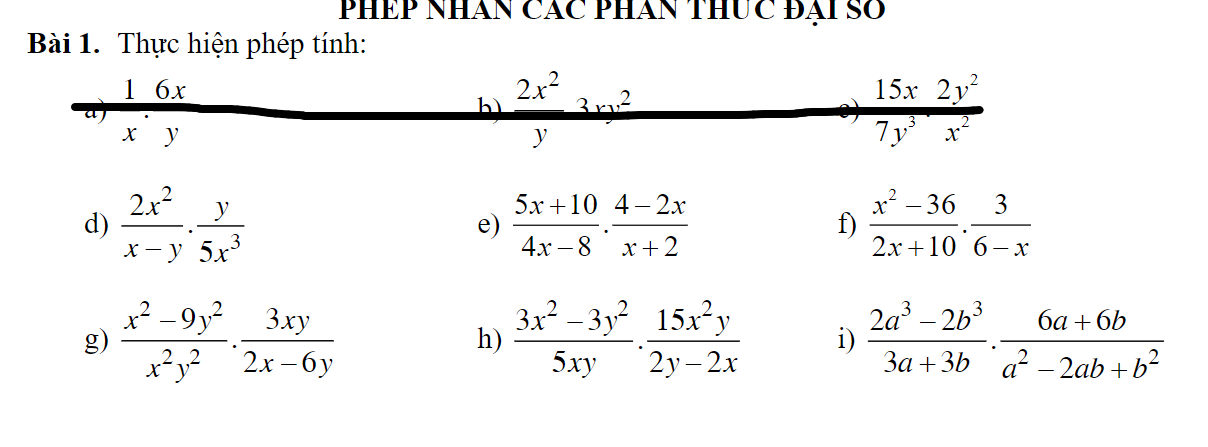
a: \(P=\left(\dfrac{2}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\right)\cdot\dfrac{\sqrt{x}}{x+\sqrt{x}+2}\)
\(=\dfrac{2\sqrt{x}+2+x-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}}{x+\sqrt{x}+2}\)
\(=\dfrac{\sqrt{x}}{x-1}\)
\(P=\left(\dfrac{2}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\right).\dfrac{\sqrt{x}}{x+\sqrt{x}+2}\)
\(\Rightarrow P=\dfrac{2\left(\sqrt{x}+1\right)+\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\dfrac{\sqrt{x}}{x+\sqrt{x}+2}\)
\(\Rightarrow P=\dfrac{x+\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\dfrac{\sqrt{x}}{x+\sqrt{x}+2}\)
\(\Rightarrow P=\dfrac{\sqrt{x}}{x-1}\)
\(\Rightarrow P=\dfrac{\sqrt{3+2\sqrt{2}}}{3+2\sqrt{2}-1}\)
\(\Rightarrow P=\dfrac{\sqrt{\left(\sqrt{2}+1\right)^2}}{2+2\sqrt{2}}\)
\(\Rightarrow P=\dfrac{\sqrt{2}+1}{2\left(\sqrt{2}+1\right)}\)
\(\Rightarrow P=\dfrac{1}{2}\)