 giúp mình câu này với mình đang cần gấp
giúp mình câu này với mình đang cần gấp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Phương trình tương đương
\(\left[{}\begin{matrix}x=\dfrac{5\pi}{12}+k\pi\\x=-\dfrac{\pi}{4}+k\pi\end{matrix}\right.,k\in Z\)
Xét họ nghiệm \(x=\dfrac{5\pi}{12}+k\pi,k\in Z\).
Do \(-\dfrac{\pi}{2}< \dfrac{5\pi}{12}+k\pi< \dfrac{8\pi}{3}\) nên \(-\dfrac{11\pi}{12}< k\pi< \dfrac{9\pi}{4}\)
⇒ \(-\dfrac{11}{12}< k< \dfrac{9}{4}\). Mà k ∈ Z nên k ∈ {0 ; 1}
Vậy các nghiệm thỏa mãn phương trình là các phần tử của tập hợp :
S1 = \(\left\{\dfrac{5\pi}{12};\dfrac{17\pi}{12}\right\}\)
Xét họ nghiệm \(x=-\dfrac{\pi}{4}+k\pi\) với k ∈ Z.
Do \(-\dfrac{\pi}{2}< \dfrac{-\pi}{4}+k\pi< \dfrac{8\pi}{3}\) nên \(-\dfrac{\pi}{4}< k\pi< \dfrac{35\pi}{12}\)
nên \(-\dfrac{1}{4}< k< \dfrac{35}{12}\). Mà k ∈ Z nên k∈ {0 ; 1 ; 2}
Vậy các nghiệm thỏa mãn phương trình là các phần tử của tập hợp
S2 = \(\left\{-\dfrac{\pi}{4};\dfrac{3\pi}{4};\dfrac{7\pi}{4}\right\}\)
Vậy các nghiệm thỏa mãn phương trình là các phần tử của tập hợp
S = S1 \(\cup\) S2 = \(\left\{\dfrac{5\pi}{12};\dfrac{17\pi}{12};-\dfrac{\pi}{4};\dfrac{3\pi}{4};\dfrac{7\pi}{4}\right\}\)

a: \(\widehat{\left(SC;\left(ABCD\right)\right)}=\widehat{CS;CA}=\widehat{SCA}\)
Ta có: SA\(\perp\)(ABCD)
=>SA\(\perp\)AC
=>ΔSAC vuông tại A
Vì ABCD là hình vuông
nên \(AC=AD\cdot\sqrt{2}=a\sqrt{2}\)
Xét ΔSAC vuông tại A có \(tanSCA=\dfrac{SA}{AC}=\dfrac{a\sqrt{6}}{a\sqrt{2}}=\sqrt{3}\)
nên \(\widehat{SCA}=60^0\)
=>\(\widehat{SC;\left(ABCD\right)}=60^0\)
b: Ta có: BD\(\perp\)AC
BD\(\perp\)SA
SA,AC cùng thuộc mp(SAC)
Do đó: BD\(\perp\)(SAC)
\(\widehat{SB;\left(SAC\right)}=\widehat{SB;SD}=\widehat{BSD}\)
Vì ABCD là hình vuông
nên \(AC=BD=a\sqrt{2}\)
ΔSAD vuông tại A
=>\(SA^2+AD^2=SD^2\)
=>\(SD^2=\left(a\sqrt{6}\right)^2+a^2=7a^2\)
=>\(SD=a\sqrt{7}\)
ΔSAB vuông tại A
=>\(SA^2+AB^2=SB^2\)
=>\(SB=a\sqrt{7}\)
Xét ΔSBD có \(cosBSD=\dfrac{SB^2+SD^2-BD^2}{2\cdot SB\cdot SD}\)
\(=\dfrac{7a^2+7a^2-2a^2}{2\cdot a\sqrt{7}\cdot a\sqrt{7}}=\dfrac{6}{7}\)
=>\(sinBSD=\sqrt{1-\left(\dfrac{6}{7}\right)^2}=\dfrac{\sqrt{13}}{7}\)
=>\(\widehat{BSD}\simeq31^0\)
=>\(\widehat{SB;\left(SAC\right)}\simeq31^0\)

\(\left(x-3\right)^{30}=\left(x-3\right)^{10}\)
\(\Leftrightarrow\left(x-3\right)\left(x-2\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=2\\x=4\end{matrix}\right.\)



đk : x khác -3
\(\left(x+3\right)^2=36\Leftrightarrow\left[{}\begin{matrix}x+3=6\\x+3=-6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-9\end{matrix}\right.\left(tm\right)\)

b: Ta có: \(\left(\dfrac{3}{5}-\dfrac{2}{3}x\right)^3=\dfrac{-64}{125}\)
\(\Leftrightarrow\dfrac{3}{5}-\dfrac{2}{3}x=\dfrac{-4}{5}\)
\(\Leftrightarrow x\cdot\dfrac{2}{3}=\dfrac{3}{5}+\dfrac{4}{5}=\dfrac{7}{5}\)
hay \(x=\dfrac{7}{5}:\dfrac{2}{3}=\dfrac{21}{10}\)

a) Cl2 + 2NaOH --> NaClO + NaCl + H2O
Chất oxh: Cl2, chất khử: Cl2
| Sự oxh | Cl0 -1e--> Cl+1 | x1 |
| Sự khử | Cl0 +1e--> Cl-1 | x1 |
b) \(n_{Cl_2}=\dfrac{17,92}{22,4}=0,8\left(mol\right);n_{NaOH}=0,5.4=2\left(mol\right)\)
PTHH: Cl2 + 2NaOH --> NaClO + NaCl + H2O
_____0,8---->1,6--------->0,8---->0,8
=> \(\left\{{}\begin{matrix}C_{M\left(NaCl\right)}=\dfrac{0,8}{0,5}=1,6M\\C_{M\left(NaClO\right)}=\dfrac{0,8}{0,5}=1,6M\\C_{M\left(NaOH\right)}=\dfrac{2-1,6}{0,5}=0,8M\end{matrix}\right.\)



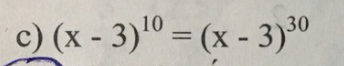 giúp mình câu này với mình đang cần gấp
giúp mình câu này với mình đang cần gấp

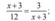
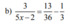
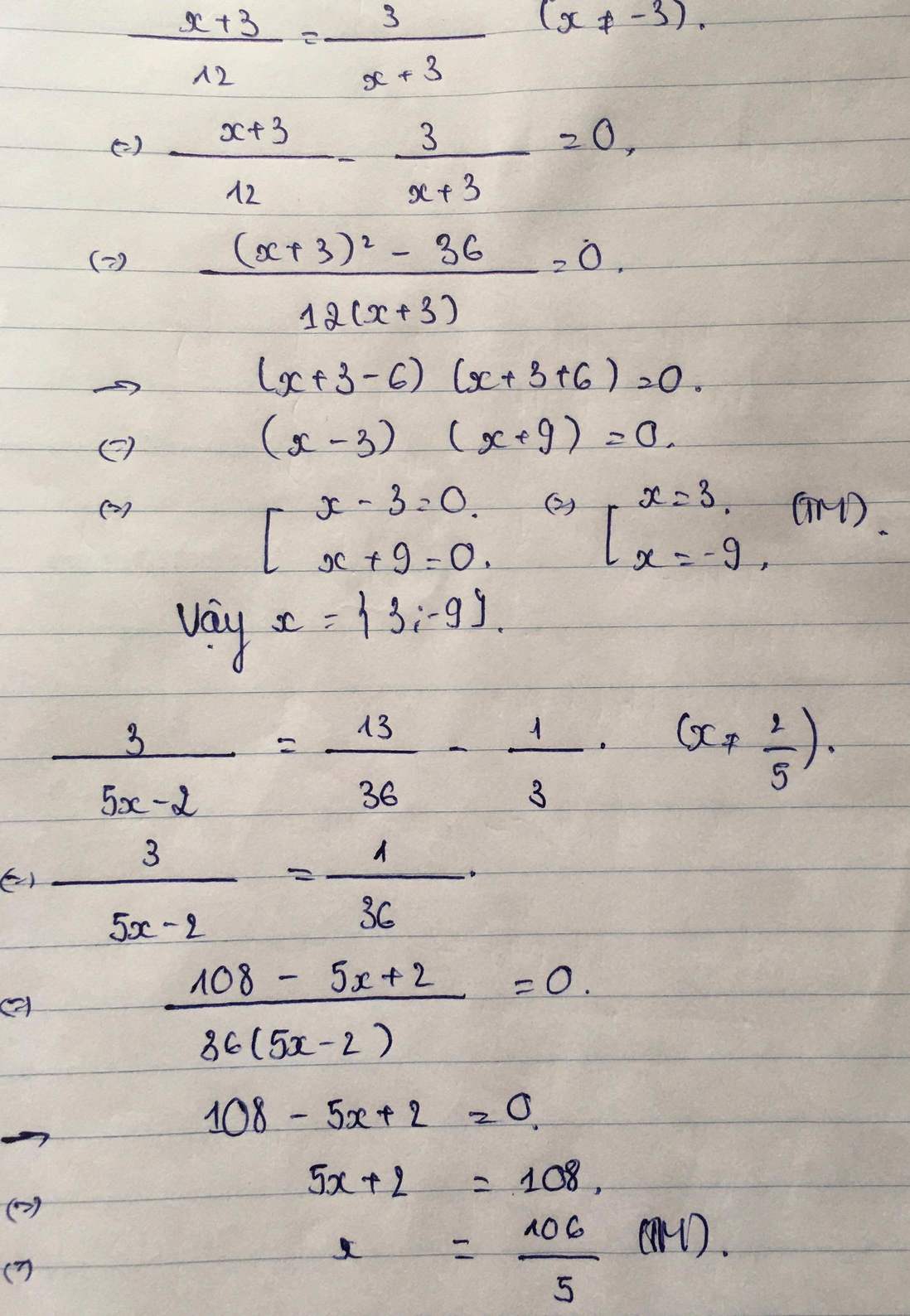
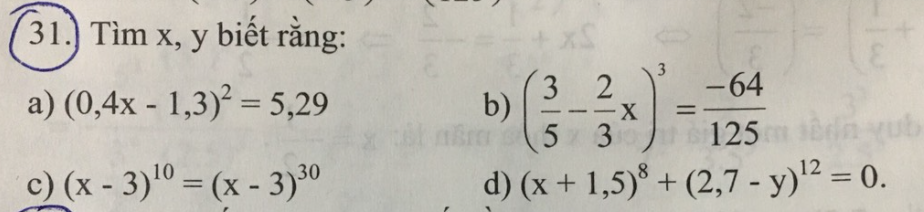 giúp mình 4 câu này với mình đang cần gấp
giúp mình 4 câu này với mình đang cần gấp 


 Giúp mình câu này với ạ, mình đang cần gấp ạ
Giúp mình câu này với ạ, mình đang cần gấp ạ