Cho hình nón có diện tích xung quanh là 140π cm2 và diện tích toàn phần của hình trụ là 190π cm2. Khi đó bán kính đáy của hình trụ bằng:
A. πR3 cm3.
B. π\(\sqrt{6}\)R3 cm3.
C. π\(\sqrt{3}\)R3 cm3.
D. 2πR3 cm3.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Gọi chiều cao của hình trụ là h
Ta có:
S x q = 2 π R 2 h ⇔ 2 π . 5 2 . h = 300 π ⇒ h = 6 ( c m )

Chọn A.
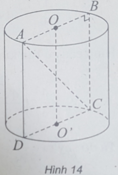
(h.14) Gọi O, O' là hai tâm của hai đáy hình trụ và thiết diện qua trục là hình chữ nhật ABCD.
Do chu vi đáy của hình trụ đó bằng 6 π (cm) nên bán kính đáy của hình trụ là: R = 3 (cm)
Vì thiết diện đi qua trục là một hình chữ nhật ABCD có AC = 10 (cm) và AB = 2R = 6 (cm) nên chiều cao của hình trụ là:
h = OO' = BC = 8 (cm)
Vậy thể tích khối trụ là: V = π R 2 h = 72 π ( cm 3 )

\(S_{xq}=140\pi\Leftrightarrow2\pi rh=140\pi\Leftrightarrow h=\dfrac{70}{r}\left(1\right)\)
\(S_{tp}=360\pi\Leftrightarrow2\pi r\left(r+h\right)=360\pi\Leftrightarrow r\left(r+h\right)=180\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow r\left(r+\dfrac{70}{r}\right)=180\\ \Leftrightarrow r^2+70=180\Rightarrow r=\sqrt{110}\)
Tổng diện tích 2 đáy là:
\(360\pi-140\pi=220\pi\left(cm^2\right)\)
Bán kính đáy hình trụ là:
\(\sqrt{\dfrac{220\pi}{2\pi}}=\sqrt{110}\) (cm2)

a, Tính được r = 1,44cm Þ Smc = 4p r 2 = 26,03 c m 2
b, Ta có V c = 4 3 πR 2 = 15 , 8 cm 3 => R = 1,56cm
=> V h n = 1 3 πR 2 h ≈ 2 , 53 πcm 3

Đáp án D
Phương pháp:

Chú ý khi giải: Khi áp dụng công thức tính diện tích xung quanh hình nón, HS thường nhầm công thức S x q = π R h dẫn đến tính nhầm tỉ số thể tích bằng 2 và chọn đáp án A là sai.

1:
V=pi*r^2*h
=>r^2*15*pi=375pi
=>r^2=25
=>r=5
Sxq=2*pi*r*h=2*5*15*pi=150pi
Đề bài không chặt chẽ lắm. Bạn xem lại đề.