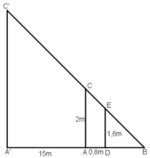
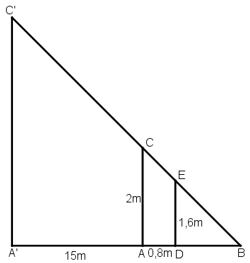
Một người đo chiều cao của một cây nhờ một cọc chôn xuống đất, cọc cao 2m và đặt xa cây 15m. sau khi người ấy lùi ra xa cách cọc 0,8m thì nhìn thấy đầu cọc và đỉnh cây cùng nằm trên một đường thẳng. Hỏi cây cao bao nhiêu, biết rằng khoảng cách từ chân đến mắt người ấy là 1,6m?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt tên các điểm như hình vẽ.
Ta có \(AB=0,8\left(m\right)\), \(BD=15\left(m\right)\), \(BC=2\left(m\right)\)
Do \(BC||DE\) (cùng vuông góc mặt đất AD)
Áp dụng định lý Thales:
\(\dfrac{AB}{AD}=\dfrac{BC}{DE}\Rightarrow\dfrac{0,8}{0,8+15}=\dfrac{2}{DE}\)
\(\Rightarrow DE=\dfrac{2.15,8}{0.8}=39,5\left(m\right)\)

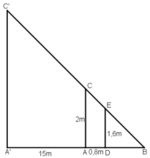
Gọi chiều cao của cây là h = A'C' và cọc tiêu AC = 2m.
Khoảng cách từ chân đến mắt người đo là DE = 1,6m.
Cọc xa cây một khoảng A'A = 15m, và người cách cọc một khoảng AD = 0,8m và gọi B là giao điểm của C'E và A'A.
Ta có: A’C’ ⊥ A’B, AC ⊥ A’B, DE ⊥ A’B
⇒ A’C’ // AC // DE.
Ta có: ΔDEB  ΔACB (vì DE // AC)
ΔACB (vì DE // AC)

Mà AB – DB = AD = 0,8
⇒ BD = 0,8.4 =3,2m; AB = 5.0,8 = 4m.
⇒ A'B = A'A + AD + DB = 15 + 0,8 + 3,2 = 19m
+ ΔACB  ΔA’C’B (vì AC // A’C’)
ΔA’C’B (vì AC // A’C’)
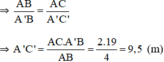
Vậy cây cao 9,5m.

Gọi chiều cao của cây là h = A'C' và cọc tiêu AC = 2m.
Khoảng cách từ chân đến mắt người đo là DE = 1,6m.
Cọc xa cây một khoảng A'A = 15m, và người cách cọc một khoảng AD = 0,8m và gọi B là giao điểm của C'E và A'A.
Ta có: A’C’ ⊥ A’B, AC ⊥ A’B, DE ⊥ A’B
⇒ A’C’ // AC // DE.
Ta có: ΔDEB  ΔACB (vì DE // AC)
ΔACB (vì DE // AC)

Mà AB – DB = AD = 0,8
⇒ BD = 0,8.4 =3,2m; AB = 5.0,8 = 4m.
⇒ A'B = A'A + AD + DB = 15 + 0,8 + 3,2 = 19m
+ ΔACB  ΔA’C’B (vì AC // A’C’)
ΔA’C’B (vì AC // A’C’)
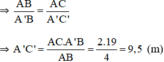
Vậy cây cao 9,5m.

Lời giải
Gọi chiều cao của cây là h = A'C' và chọn một cọc tiêu AC = 2m.
Khoảng cách từ chân đến mắt người đo là DE = 1,6m.
Cọc xa cây một khoảng A'A = 15m, và người cách cọc một khoảng AD = 0,8m và gọi B là giao điểm của C'E và A'A.
Giải:
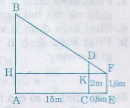
Giả sử AB là cây cần do, CD là cọc EF là khoảng cách từ mắt tới chân.
∆KDF ∽ ∆HBF
=> HBKD=HFKFHBKD=HFKF
=> HB = HF.KDKFHF.KDKF
mà HF = HK + KF =AC + CE = 15 + 0,8 = 15.8m
KD = CD - CK = CD - EF = 2 - 1,6 = 0,4 m
Do đó: HB = 7,9 m
Vậy chiều cao của cây là 7,9 m.

Gọi chiều cao của cây là h = A'C' và cọc tiêu AC = 2m.
Khoảng cách từ chân đến mắt người đo là DE = 1,6m.
Cọc xa cây một khoảng A'A = 15m, và người cách cọc một khoảng AD = 0,8m và gọi B là giao điểm của C'E và A'A.
Ta có: A’C’ ⊥ A’B, AC ⊥ A’B, DE ⊥ A’B
⇒ A’C’ // AC // DE.
Ta có: ΔDEB 
Mà AB – DB = AD = 0,8
⇒ BD = 0,8.4 =3,2m; AB = 5.0,8 = 4m.
⇒ A'B = A'A + AD + DB = 15 + 0,8 + 3,2 = 19m
+ ΔACB 
Vậy cây cao 9,5m.

Gọi chiều cao của cây là h = A'C' và cọc tiêu AC = 2m.
Khoảng cách từ chân đến mắt người đo là DE = 1,6m.
Cọc xa cây một khoảng A'A = 15m, và người cách cọc một khoảng AD = 0,8m và gọi B là giao điểm của C'E và A'A.
Ta có: A’C’ ⊥ A’B, AC ⊥ A’B, DE ⊥ A’B
⇒ A’C’ // AC // DE.
Ta có: ΔDEB 
\(\Rightarrow\frac{DE}{AC}=\frac{DB}{AB}\)
Mà AC = 2m , DE = 1,6m
nên \(\frac{1,6}{2}=\frac{DB}{AB}\Rightarrow\frac{DB}{AB}=\frac{4}{5}\Rightarrow\frac{DB}{4}=\frac{AB}{5}\)
Áp dụng t/c DTSBN , ta có:
\(\frac{DB}{4}=\frac{AB}{5}=\frac{AB-DB}{5-4}=\frac{AD}{1}=0,8\)
Suy ra :
\(\frac{DB}{4}=0,8\Rightarrow DB=0,8.4=3,2\)
\(\frac{AB}{5}=0,8\Rightarrow AB=0,8.5=4\)
Mà AB – DB = AD = 0,8
⇒ BD = 0,8.4 =3,2m; AB = 5.0,8 = 4m.
⇒ A'B = A'A + AD + DB = 15 + 0,8 + 3,2 = 19m
+ ΔACB ~ ΔA’C’B (vì AC // A’C’)
\(\Rightarrow\frac{AB}{A'B'}=\frac{AC}{A'C'}\)
\(\Rightarrow AC=\frac{AC.A'B'}{AB}=\frac{2.19}{4}=9,5\left(m\right)\)
Vậy cây cao 9,5m

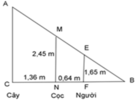
Ta mô tả vị trí cây, cọc và người như hình vẽ bên.
Xét ΔBFE và ΔBNM ta có:
B chung
B E F ^ = B M N ^ (vì EF // MN, cặp góc đồng vị bằng nhau)
=> ΔBFE ~ ΔBNM (g - g)
⇒ B F B N = F E N M ⇔ B F B F + F N = F E N M ⇔ B F B F + 0 , 64 = 1 , 65 2 , 45
⇔ 1,65(BF + 0,64) = 2,45.BF
⇔ BF = 1,32m
Xét ΔBFE và ΔBCA có:
B chung
B E F ^ = B A C ^ (vì EF // AC, cặp góc đồng vị bằng nhau)
=> ΔBFE ~ ΔBCA (g - g)
⇒ B F B C = F E C A ⇔ B F B F + F N + N C = F E C A ⇔ 1 , 32 1 , 32 + 0 , 64 + 1 , 36 = 1 , 65 C A
=> CA = 4,15m
Vậy cây cao đúng bằng độ dài của đoạn CA hay cây cao 4,15m.
Đáp án: D
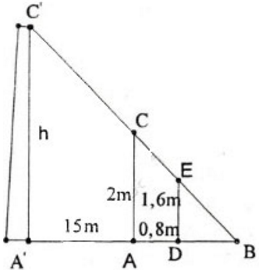


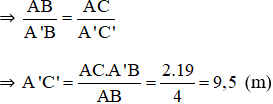
Đáp án:
Giải thích các bước giải:
Giả sử AB là cây cần do, CD là cọc EF là khoảng cách từ mắt tới chân.
∆KDF ∽ ∆HBF
=> HBKD=HFKFHBKD=HFKF
=> HB = HF.KDKFHF.KDKF
mà HF = HK + KF =AC + CE = 15 + 0,8 = 15.8m
KD = CD – CK = CD – EF = 2 – 1,6 = 0,4 m
Do đó: HB = 7,9 m
Vậy chiều cao của cây là 7,9