Chuyên ĐHSP HN ( 2014)
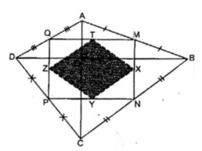
5. Cho hình vuông ABCD với tâm O. Gọi M là trung điểm của cạnh AB. Các điểm N, P theo thứ tự thuộc cạnh BC,CD sao cho MN//AP. Chứng minh rằng:
a) \(\Delta BNO~\Delta DOP\) và ^NOP = 45o
b) Tâm đường tròn ngoại tiếp tam giác NOP thuộc OC
c) Ba đường thẳng BD, AN, PM đồng quy.

\(x = {-b \pm \sqrt{b^2-4ac} \over 2a}\) fhhhhhhhhh