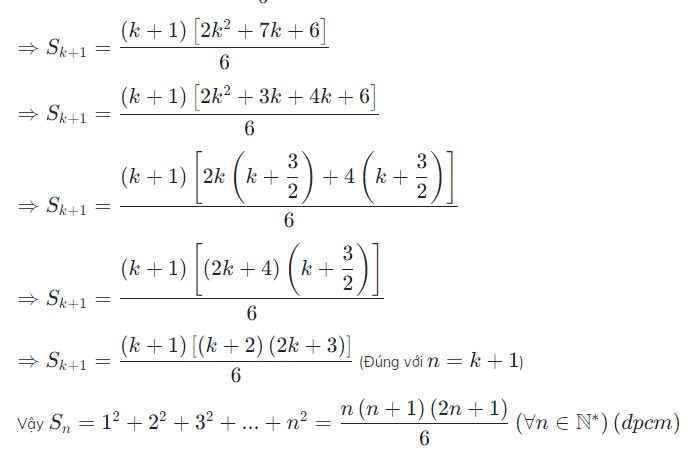Chứng minh rằng với mọi số tự nhiên n, ta có: (n + 1)(n + 2)...(n + n) = \(^{2^n}\).1.3.5...(2n -1)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 10 2023
Bước 1: Chứng minh công thức đúng cho n = 1. Khi n = 1, ta có: 1² = 1 = 1 . (1 + 1) . (2 . 1 + 1) / 6 = 1. Vậy công thức đúng cho n = 1.
Bước 2: Giả sử công thức đúng cho n = k, tức là 1² + 2² + ... + k² = k . (k + 1) . (2k + 1) / 6. Ta cần chứng minh công thức đúng cho n = k + 1, tức là 1² + 2² + ... + k² + (k + 1)² = (k + 1) . (k + 1 + 1) . (2(k + 1) + 1) / 6.
Bước 3: Chứng minh công thức đúng cho n = k + 1. Ta có: 1² + 2² + ... + k² + (k + 1)² = (k . (k + 1) . (2k + 1) / 6) + (k + 1)² = (k . (k + 1) . (2k + 1) + 6(k + 1)²) / 6 = (k . (k + 1) . (2k + 1) + 6(k + 1) . (k + 1)) / 6 = (k + 1) . ((k . (2k + 1) + 6(k + 1)) / 6) = (k + 1) . ((2k² + k + 6k + 6) / 6) = (k + 1) . ((2k² + 7k + 6) / 6) = (k + 1) . ((k + 2) . (2k + 3) / 6) = (k + 1) . ((k + 1 + 1) . (2(k + 1) + 1) / 6).
Vậy, công thức đã được chứng minh đúng cho mọi số tự nhiên n khác 0.
PT
1
CM
13 tháng 4 2018
* Với n = 2 ta có 2 2 + 1 > 2.2 + 3 ⇔ 8 > 7 (đúng).
Vậy (*) đúng với n= 2 .
* Giả sử với n = k , k ≥ 2 thì (*) đúng, có nghĩa ta có: 2 k + 1 > 2 k + 3 (1).
* Ta phải chứng minh (*) đúng với n = k + 1, có nghĩa ta phải chứng minh:
2 k + 2 > 2 ( k + 1 ) + 3
Thật vậy, nhân hai vế của (1) với 2 ta được:
2.2 k + 1 > 2 2 k + 3 ⇔ 2 k + 2 > 4 k + 6 > 2 k + 5 .
( vì 4k + 6 > 4k + 5 > 2k + 5 )
Hay 2 k + 2 > 2 ( k + 1 ) + 3
Vậy (*) đúng với n = k + 1 .
Do đó theo nguyên lí quy nạp, (*) đúng với mọi số nguyên dương ≥ 2
AD
0
11 tháng 12 2023
a:
\(1^2+2^2+3^2+...+n^2=\dfrac{n\left(n+1\right)\left(2n+1\right)}{6}\left(1\right)\)
Đặt \(S=1^2+2^2+...+n^2\)
Với n=1 thì \(S_1=1^2=1=\dfrac{1\left(1+1\right)\left(2\cdot1+1\right)}{6}\)
=>(1) đúng với n=1
Giả sử (1) đúng với n=k
=>\(S_k=1^2+2^2+3^2+...+k^2=\dfrac{k\left(k+1\right)\left(2k+1\right)}{6}\)
Ta sẽ cần chứng minh (1) đúng với n=k+1
Tức là \(S_{k+1}=\dfrac{\left(k+1+1\right)\cdot\left(k+1\right)\left(2\cdot\left(k+1\right)+1\right)}{6}\)
Khi n=k+1 thì \(S_{k+1}=1^2+2^2+...+k^2+\left(k+1\right)^2\)
\(=\dfrac{k\left(k+1\right)\left(2k+1\right)}{6}+\left(k+1\right)^2\)
\(=\left(k+1\right)\left(\dfrac{k\left(2k+1\right)}{6}+k+1\right)\)
\(=\left(k+1\right)\cdot\dfrac{2k^2+k+6k+6}{6}\)
\(=\left(k+1\right)\cdot\dfrac{2k^2+3k+4k+6}{6}\)
\(=\dfrac{\left(k+1\right)\cdot\left[k\left(2k+3\right)+2\left(2k+3\right)\right]}{6}\)
\(=\dfrac{\left(k+1\right)\left(k+2\right)\left(2k+3\right)}{6}\)
\(=\dfrac{\left(k+1\right)\left(k+1+1\right)\left[2\left(k+1\right)+1\right]}{6}\)
=>(1) đúng
=>ĐPCM
b: \(A=1\cdot5+2\cdot6+3\cdot7+...+2023\cdot2027\)
\(=1\left(1+4\right)+2\left(2+4\right)+3\left(3+4\right)+...+2023\left(2023+4\right)\)
\(=\left(1^2+2^2+3^2+...+2023^2\right)+4\left(1+2+2+...+2023\right)\)
\(=\dfrac{2023\cdot\left(2023+1\right)\left(2\cdot2023+1\right)}{6}+4\cdot\dfrac{2023\left(2023+1\right)}{2}\)
\(=\dfrac{2023\cdot2024\cdot4047}{6}+\dfrac{2023\cdot2024}{1}\)
\(=2023\left(\dfrac{2024\cdot4047}{6}+2024\right)⋮2023\)
\(A=\dfrac{2023\cdot2024\cdot4047}{6}+2023\cdot2024\)
\(=2024\left(2023\cdot\dfrac{4047}{6}+2023\right)\)
\(=23\cdot11\cdot8\cdot\left(2023\cdot\dfrac{4047}{6}+2023\right)\)
=>A chia hết cho 23 và 11
PT
1
CM
15 tháng 10 2019
2n + 1 > 2n + 3 (2)
+ Với n = 2 thì (2) ⇔ 8 > 7 (luôn đúng).
+ Giả sử (2) đúng khi n = k ≥ 2, nghĩa là 2k+1 > 2k + 3.
Ta chứng minh đúng với n= k+ 1 tức là chứng minh: 2k+2 > 2(k+ 1)+ 3
Thật vậy, ta có:
2k + 2 = 2.2k + 1
> 2.(2k + 3) = 4k + 6 = 2k + 2 + 2k + 4.
> 2k + 2 + 3 = 2.(k + 1) + 3 ( Vì 2k + 4 >3 với mọi k ≥ 2)
⇒ (2) đúng với n = k + 1.
Vậy 2n + 1 > 2n + 3 với mọi n ≥ 2.