cho tam giác ABC vuông cân tại A. Dựng tam giác DEF vuông cân tại D có D thuộc AB, E thuộc AC, F thuộc BC. chứng minh: \(_{S_{DEF}=\frac{1}{5}S_{ABC}}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 1 2019
Từ A hạ AH vuông góc với BC tại H. Gọi M là trung điểm cạnh BC. Nối MD cắt EF tại O.
Bằng 2 bổ đề đơn giản, ta dễ thấy:
\(\Delta\)MEF vuông cân (Gợi ý: Hạ EP vuông góc AB, FQ vuông góc AC)
Và HF là phân giác ^AHC (Gợi ý: Kẻ FI vuông góc AH và FK vuông góc BC)
Từ \(\Delta\)MEF vuông cân (tại M) kết hợp với \(\Delta\)DEF vuông cân
=> Tứ giác MEDF là hình vuông => OM=OD=OE=OF (1)
Từ HF là phân giác ^AHC, tương tự thì HE là phân giác ^AHB => ^EHF = (^AHB + ^AHC)/2 = 900
=> \(\Delta\)HEF vuông tại H có trung tuyến HO nên OH = OE=OF (2)
Từ (1) và (2) suy ra: OH=OD=OM => \(\Delta\)DHM vuông tại H hay DH vuông góc BC
Mà AH cũng vuông góc BC nên tia HA trùng HD => 3 điểm D,A,H thẳng hàng.
Dẫn đến AD cũng vuông góc BC (đpcm).
26 tháng 8 2023
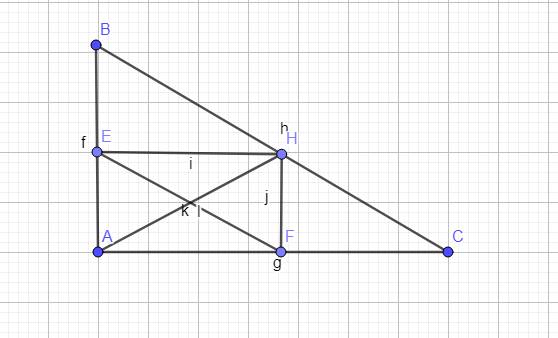
Ta có: tam giác vuông EBH \(\sim\) tam giác vuông ABC (gt)
=>\(\dfrac{S\Delta EBH}{S\Delta ABC}=\left(\dfrac{BH}{BC}\right)^2\Rightarrow\dfrac{\sqrt{S\Delta EBH}}{\sqrt{S\Delta ABC}}=\dfrac{BH}{BC}\left(1\right)\)
Ta có tam giác vuông FHC \(\sim\) tam giác vuông ABC (g.g)
=>\(\dfrac{S\Delta FHC}{S\Delta ABC}=\left(\dfrac{HC}{BC}\right)^2\Rightarrow\dfrac{\sqrt{S\Delta FHC}}{\sqrt{S\Delta ABC}}=\dfrac{HC}{BC}\left(2\right)\)
\(\)Từ (1)và (2) =>\(\dfrac{\sqrt{S\Delta EBH}+\sqrt{S\Delta FHC}}{\sqrt{S\Delta ABC}}=\dfrac{HB+HC}{BC}=\dfrac{BC}{BC}=1\)
Vậy \(\sqrt{S\Delta_{EBH}}+\sqrt{S\Delta_{FHC}}=\sqrt{S\Delta_{ABC}}\left(đpcm\right)\)
chucbanhoctot!
26 tháng 8 2023
thực ra ở đây ko thể c/m đc yêu cầu của bạn đâu, cần phải có AEHF là hcn mới ra cơ ạ
11 tháng 5 2023
a: Xét ΔADB và ΔADC có
AB=AC
góc BAD=góc CAD
AD chung
=>ΔADB=ΔADC
b: Xét ΔAED vuông tại E và ΔAFD vuông tại F có
AD chung
góc EAD=góc FAD
=>ΔAED=ΔAFD
=>AE=AF và DE=DF
c: Xét ΔABC có AE/AB=AF/AC
nên EF//BC
8 tháng 1
a: Xét ΔABD vuông tại D và ΔACD vuông tại C có
AB=AC
AD chung
Do đó: ΔABD=ΔACD
=>DB=DC
=>D là trung điểm của BC
b: Xét ΔAED vuông tại E và ΔAFD vuông tại F có
AD chung
\(\widehat{EAD}=\widehat{FAD}\)(ΔABD=ΔACD)
Do đó: ΔAED=ΔAFD
=>AE=AF
=>ΔAEF cân tại A
16 tháng 9 2023
a: Xét ΔADB và ΔADC có
AB=AC
góc BAD=góc CAD
AD chung
=>ΔADB=ΔADC
b: Xét ΔAED vuông tại E và ΔAFD vuông tại F có
AD chung
góc EAD=góc FAD
=>ΔAED=ΔAFD
=>AE=AF và DE=DF
c: Xét ΔABC có AE/AB=AF/AC
nên EF//BC