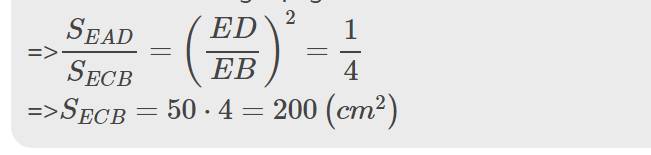Cho tam giác ABC vuông tại A AB = 6 AC = 8 lấy M thuộc AC, AM=AB.Kẻ ME vuông góc với BC tại E.
a) cm: CM.CA=CE.CB
b) tia BA và EM cắt nhau tại N. Đường thẳng BM cắt NC tại F. Cm tam giác AMB dồng dạng với tam giác FMC. cm tam giác ANC vuông cân
c) tính SBFN/SMFC