Bài 1: Một người đi xe máy từ tỉnh A đến tỉnh B với vận tốc dự định là 40 km/h . Sau khi đi đc 1 giờ với vận tốc ấy, người đó nghỉ 15 phút và tiếp tục đi. Để đến B kịp thời gian đã định, người đó phải tăng vận tốc thêm 5km/h. Tính quãng đường từ tỉnh A đến tỉnh B .
Bài 2: Một ôtô chạy trên quãng đường AB . Lúc đi từ A đến B ôtô chạy với vận tốc 40km/h, lúc về từ B đến A ôtô...
Đọc tiếp
Bài 1: Một người đi xe máy từ tỉnh A đến tỉnh B với vận tốc dự định là 40 km/h . Sau khi đi đc 1 giờ với vận tốc ấy, người đó nghỉ 15 phút và tiếp tục đi. Để đến B kịp thời gian đã định, người đó phải tăng vận tốc thêm 5km/h. Tính quãng đường từ tỉnh A đến tỉnh B .
Bài 2: Một ôtô chạy trên quãng đường AB . Lúc đi từ A đến B ôtô chạy với vận tốc 40km/h, lúc về từ B đến A ôtô chạy với vận tốc 50km/h, vì vậy thời gian về ít hơn thời gian đi là 1/2 giớ . Tính độ dài quãng đường AB .
Bài 3: Trên quãng đường AB dài 30km, một người đi từ A đến C với vận tốc 30km/h , rồi đi từ C đến B với vận tốc 20km/h hết tất cả 1 giờ 10 phút. Tính quãng đường AC và CB.
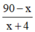(h).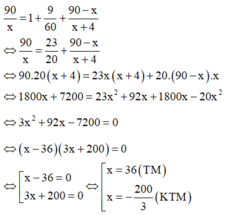
Bài 1:
Gọi x (km) là quãng đường AB (x > 0)
Thời gian dự định đi: \(\frac{x}{40}\left(h\right)\)
Quãng đường còn phải đi sau khi đã đi 1 giờ: x - 40 (km)
Vận tốc mới: 40 + 5 = 45 (km/h)
Thời gian đi đến B với vận tốc mới: \(\frac{x-40}{45}\left(h\right)\)
Đổi: 15 phút = \(\frac{1}{4}\left(h\right)\)
Theo đề bài, ta có phương trình:
\(1+\frac{1}{4}+\frac{x-40}{45}=\frac{x}{40}\)
Sau khi quy đồng, khử mẫu và rút gọn ta sẽ có:
5x = 650
⇒ x = 130 (TMĐK)
Vậy quãng đường AB dài 130 (km)