Bài 1:
a/ Vẽ trên cùng một mặt phẳng tọa độ đồ thị 2 hàm số sau:
(\(d_1\)): y=x-3 ; (\(d_2\)): y=2x+1
b/ Tìm tọa độ giao điểm của (\(d_1\)) và (\(d_2\))
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: Khi m=1 thì (d1): y=x+3 và (d2): y=-x+3
a: 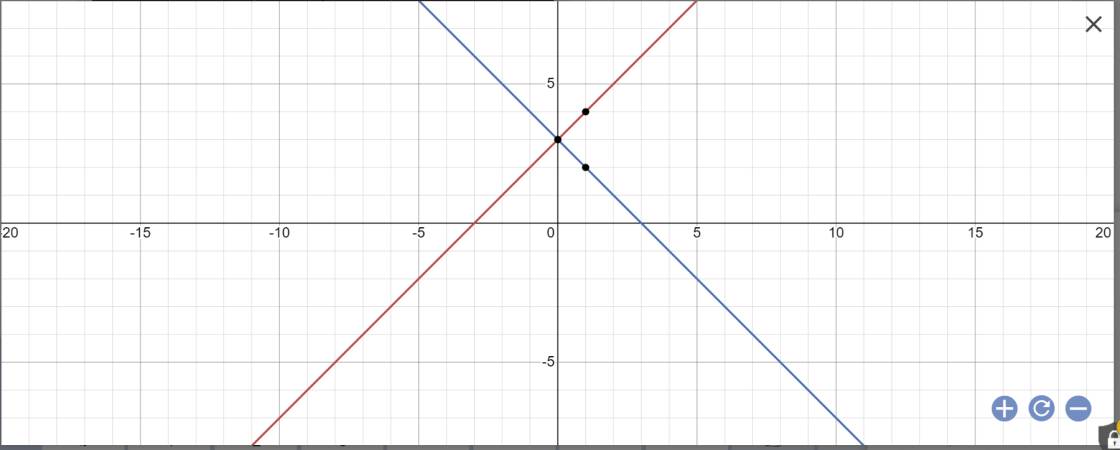
b: Tọa độ giao điểm là:
x+3=-x+3 và y=x+3
=>x=0 và y=3

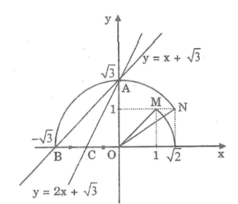
*Vẽ đồ thị của hàm số y = x + 3
Cho x = 0 thì y = 3 . Ta có: A(0; 3 )
Cho y = 0 thì x + 3 = 0 => x = - 3 . Ta có: B(- 3 ; 0)
Cách tìm điểm có tung độ bằng 3 trên trục Oy:
- Dựng điểm M(1; 1). Ta có: OM = 2
- Dựng cung tròn tâm O bán kính OM cắt trục OX tại điểm có hoành độ bằng 2
- Dựng điểm N(1; 2 ). Ta có: ON = 3
- Vẽ cung tròn tâm O bán kính ON cắt trục Oy tại A có tung độ 3 cắt tia đối của Ox tại B có hoành độ -3
Đồ thị của hàm số y = x + 3 là đường thẳng AB.
*Vẽ đồ thị của hàm số y = 2x + 3
Cho x = 0 thì y = 3 . Ta có: A(0; 3 )
Cho y = 0 thì 2x + 3 = 0 => x = - 3 /2 . Ta có: C(- 3 /2 ; 0)
Đồ thị của hàm số y = 2x + 3 là đường thẳng AC.

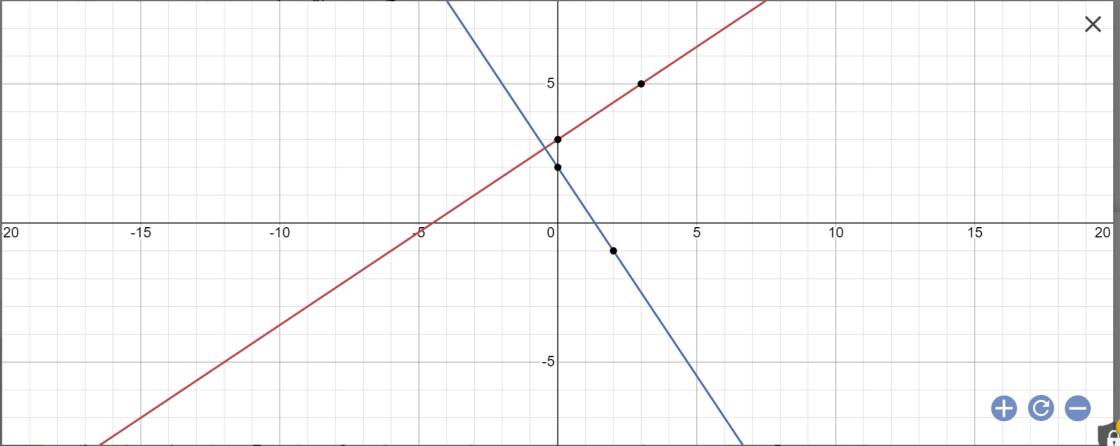
2. PT hoành độ giao điểm: \(3x=x+2\Leftrightarrow2x=2\Leftrightarrow x=1\Leftrightarrow y=3\Leftrightarrow A\left(1;3\right)\)
Vậy \(A\left(1;3\right)\) là giao 2 đths

Bảng giá trị:
| x | -1 | 0 | 1 |
| \(y=\dfrac{2}{3}x+3\) | \(\dfrac{7}{3}\) | 3 | \(\dfrac{11}{3}\) |
| \(y=-\dfrac{3}{2}x+2\) | \(\dfrac{7}{2}\) | 2 | \(\dfrac{1}{2}\) |
Vẽ đồ thị:

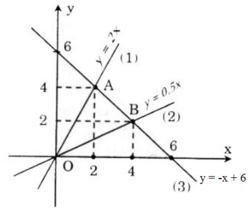
– Vẽ đồ thị y = 2x (1):
Cho x= 0 ⇒ y= 0 ta được O (0, 0)
Cho x= 2 ⇒ y = 4 ta được điểm (2; 4)
- Vẽ đồ thị y = 0,5x (2):
Cho x= 0 ⇒ y = 0 ta được O (0; 0)
Cho x = 4 ⇒ y = 2 ta được điểm (4; 2)
- Vẽ đồ thị y = -x + 6 (3):
Cho x = 0 ⇒ y = 6 được điểm (0; 6)
Cho y = 0 ⇒ x = 6 được điểm (6; 0)
b: Phương trình hoành độ giao điểm là:
2x+1=x-3
hay x=-4
Thay x=-4 vào y=x-3, ta được:
y=-4-3=-7