Tìm các giá trị m để tam thức f(x)=\(x^2-\left(m+2\right)x+8m+1\) đổi dấu hai lần
A. m<0 hoặc m>28
B. m\(\le\)0 hoặc m\(\ge\)28
C. 0<m<28
D. m>0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: B
Tam thức f(x) = x 2 - (m + 2)x + 8m + 1 đổi dấu hai lần khi và chỉ khi f(x) có hai nghiệm phân biệt
Ta có: Δ = [-(m + 2) ] 2 - 4.(8m + 1) = m 2 - 28m
f(x) có hai nghiệm phân biệt khi và chỉ khi
Δ > 0 ⇔
m
2
- 28m > 0 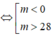

\(f\left(x\right)=x^2-\left(m+2\right)x+8m+1>0\) với mọi x
\(\Leftrightarrow\left\{{}\begin{matrix}a>0\\\Delta< 0\end{matrix}\right.\)
\(\Leftrightarrow\left(m+2\right)^2-4\left(8m+1\right)< 0\)
\(\Leftrightarrow m^2+4m+4-32m-4< 0\)
\(\Leftrightarrow m^2-28m< 0\)
\(\Leftrightarrow0< m< 28\)

Không có đáp án đúng. Theo đáp án thì $m=0$ thì $\sin 2x=2m$ có 2 nghiệm pb thuộc $[0;\pi]$
Tức là $\sin 2x=0$ có 2 nghiệm pb $[0;\pi]$. Mà pt này có 3 nghiệm lận:
$x=0$
$x=\frac{1}{2}\pi$
$x=\pi$

a) điều kiện cần và đủ \(\Delta< 0\Rightarrow\left(m+2\right)^2-8\left(m^2-m-1\right)< 0\)
\(\Leftrightarrow-7m^2+12m+12< 0\) \(\Rightarrow\left[{}\begin{matrix}m< \dfrac{6-2\sqrt{30}}{7}\\m>\dfrac{6+2\sqrt{30}}{7}\end{matrix}\right.\)
b) ????
b) Xét \(m^2-m-1=0\)\(\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{1+\sqrt{5}}{2}\\m=\dfrac{1-\sqrt{5}}{2}\end{matrix}\right.\)
Với \(m=\dfrac{1+\sqrt{5}}{2}\) thay vào phương trình ta có:\(-\sqrt{5}x+1\)
Do \(-\sqrt{5}x+1>0\Leftrightarrow x< \dfrac{1}{\sqrt{5}}\) vì vậy \(m=\dfrac{1+\sqrt{5}}{2}\) không thỏa mãn.
Tương tự với \(m=\dfrac{1-\sqrt{5}}{2}\).
Xét \(m^2-m-1\ne0\) \(\Leftrightarrow\left\{{}\begin{matrix}m\ne\dfrac{1+\sqrt{5}}{2}\\m\ne\dfrac{1-\sqrt{5}}{2}\end{matrix}\right.\).
Có \(\Delta=\left(2m-1\right)^2-4.\left(m^2-m-1\right)=5>0\).
Do vậy tam thức bậc hai luôn có hai nghiệm phân biệt nên dấu của tam thức sẽ phụ thuộc vào x.
Kết luận: Không có giá trị nào thỏa mãn.
Để tam thức đổi dấu 2 lần
\(\Leftrightarrow x^2-\left(m+2\right)x+8m+1=0\) có 2 nghiệm pb
\(\Leftrightarrow\Delta=\left(m+2\right)^2-4\left(8m+1\right)>0\)
\(\Leftrightarrow m^2-28m>0\Rightarrow\left[{}\begin{matrix}m>28\\m< 0\end{matrix}\right.\)
Đổi dấu 2 lần nghĩa là sao ạ? :(