Cho tam giác ABC vuông cân tại A. Qua điểm D ϵ cạnh BC, kẻ đường thẳng vuông góc với BC, cắt cạnh AB, AC theo thứ tự ở E và F. Gọi M, N là thứ tự theo trung điểm của BE và CF. CMR:
a) Tứ giác AMDN là hình chữ nhật?
b) AD=MN?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

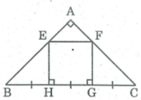
Vì ΔABC vuông cân tại A nên ∠ B = ∠ C = 45 0
Vì ΔBHE vuông tại H có ∠ B = 45 0 nên ΔBHE vuông cân tại H.
Suy ra HB = HE
Vì ΔCGF vuông tại G, có ∠ C = 45 0 nên ΔCGF vuông cân tại G
Suy ra GC = GF
Ta có: BH = HG = GC (gt)
Suy ra: HE = HG = GF
Vì EH // GF (hai đường thẳng cũng vuông góc với đường thắng thứ ba) nên tứ giác HEFG là hình bình hành (vì có một cặp cạnh đối song song bằng nhau);
Lại có ∠ (EHG) = 90 0 nên HEFG là hình chữ nhật.
Mà EH = HG (chứng minh trên).
Vậy HEFG là hình vuông.

Tam giác vuông FGC có \(\widehat{C}=45^0\) nên là tam giác vuông cân. Do đó FG = GC


a: ΔHEB vuông tại H có góc HBE=45 độ
nên ΔHEB vuông cân tại H
b: KH//AB
=>gó KHE=góc HEB=45 độ
=>ΔKHM vuôngtại K
=>KH=KM
ΔCKH vuông tại K có góc C=45 độ
nên ΔCKH vuông cân tại K
=>KC=KH=KM
=>K là trung điểm của MC

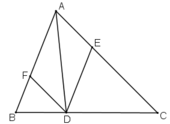
a) Tứ giác AEDF là hình bình hành.
Vì có DE // AF, DF // AE (gt) (theo định nghĩa)
b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A. Vậy nếu D là giao điểm của tia phân giác góc A với cạnh BC thì AEDF là hình thoi.
c) Nếu ΔABC vuông tại A thì AEDF là hình chữ nhật (vì là hình bình hành có một góc vuông).
d) Nếu ABC vuông tại A và D là giao điểm của tia phân giác của góc A với cạnh BC thì AEDF là hình vuông (vì vừa là hình chữ nhật, vừa là hình thoi).

Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
=>ADHE là hình chữ nhật
=>\(\widehat{AED}=\widehat{AHD}\)
AM\(\perp\)DE
=>\(\widehat{AED}+\widehat{MAC}=90^0\)
mà \(\widehat{AED}=\widehat{AHD}\left(cmt\right)\)
và \(\widehat{AHD}=\widehat{ABH}\left(=90^0-\widehat{HAB}\right)\)
nên \(\widehat{ABH}+\widehat{MAC}=90^0\)
mà \(\widehat{ABH}+\widehat{MCA}=90^0\)(ΔABC vuông tại A)
nên \(\widehat{MAC}=\widehat{MCA}\)
=>MA=MC
\(\widehat{MAC}+\widehat{MAB}=\widehat{BAC}=90^0\)
\(\widehat{MCA}+\widehat{MBA}=90^0\)(ΔABC vuông tại A)
mà \(\widehat{MAC}=\widehat{MCA}\)
nên \(\widehat{MAB}=\widehat{MBA}\)
=>MA=MB
mà MA=MC
nên MB=MC
=>M là trung điểm của BC
( Hình em tự vẽ nhé! )
Lấy O là giao điểm DE và HA
+ Xét tứ giác ADHE có:
\(\widehat{HDA}=\widehat{DAE}=\widehat{AEH}=90^o\)
=> ADHE là hình chữ nhật
=> O là trung điểm AH (t/c)
O là trung điểm DE (t/c)
=> OA = OH = OD = OE
=> ΔAOE cân tại O
=> \(\widehat{OAE}=\widehat{OEA}\left(tc\right)\)
+ Xét ΔABH vuông tại H
=> \(\widehat{BAH}+\widehat{ABH}=90^o\)
Mà \(\widehat{BAH}+\widehat{CAH}=90^o\)
=> \(\widehat{ABH}=\widehat{CAH}\)
Mà \(\widehat{CAH}=\widehat{OEH}\)
\(\widehat{ABH}=\widehat{AEO}\)
+ Xét ΔADE và ΔACB có:
\(\widehat{DAE}=\widehat{CAB}\left(=90^o\right)\)
\(\widehat{AED}=\widehat{ABC}\)
=> ΔADE \(\sim\) ΔACB (g.g)
=> \(\widehat{ADE}=\widehat{ACB}\left(2gtu\right)\)
Lấy I là giao điểm AM và DE
+ Xét ΔAIE vuông tại I
=> \(\widehat{IAE}+\widehat{IEA}=90^o\)
Mà \(\widehat{BAM}+\widehat{MAC}=90^o\)
=> \(\widehat{IEA}=\widehat{MAB}\)
Mà \(\widehat{IEA}=\widehat{ABC}\)
=> \(\widehat{ABC}=\widehat{BAM}\)
=> ΔABM cân tại M
=> MA = MB (t/c)
+ Xét ΔAID vuông tại I
=> \(\widehat{IDA}+\widehat{IAD}=90^o\)
Mà \(\widehat{IAD}+\widehat{MAC}=90^o\)
=> \(\widehat{IDA}=\widehat{MAC}\)
Mà \(\widehat{IDA}=\widehat{ACM}\)
=> \(\widehat{MAC}=\widehat{ACM}\)
=> ΔMAC cân tại M
=> MA = MC (t/c)
Mà MA = MB
=> MB = MC
=> M là trung điểm BC.

a: Xét tứ giác BPQC có
\(\widehat{BPC}=\widehat{BQC}=90^0\)
Do đó: BPQC là tứ giác nội tiếp

Sửa đề: BF và CE cắt nhau tại H
a) Xét (O) có
ΔBEC nội tiếp đường tròn(B,E,C\(\in\)(O))
BC là đường kính(gt)
Do đó: ΔBEC vuông tại E(Định lí)
\(\Leftrightarrow CE\perp BE\)
\(\Leftrightarrow CE\perp AB\)
\(\Leftrightarrow\widehat{AEC}=90^0\)
hay \(\widehat{AEH}=90^0\)
Xét (O) có
ΔBFC nội tiếp đường tròn(B,F,C\(\in\)(O))
BC là đường kính(gt)
Do đó: ΔBFC vuông tại F(Định lí)
\(\Leftrightarrow BF\perp CF\)
\(\Leftrightarrow BF\perp AC\)
\(\Leftrightarrow\widehat{AFB}=90^0\)
hay \(\widehat{AFH}=90^0\)
Xét tứ giác AEHF có
\(\widehat{AEH}\) và \(\widehat{AFH}\) là hai góc đối
\(\widehat{AEH}+\widehat{AFH}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: AEHF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Xét ΔABC có
BF là đường cao ứng với cạnh AC(cmt)
CE là đường cao ứng với cạnh AB(cmt)
BF cắt CE tại H(gt)
Do đó: H là trực tâm của ΔABC(Định lí ba đường cao của tam giác)
\(\Leftrightarrow AH\perp BC\)
hay \(AD\perp BC\)(đpcm)
ủa, bạn tên đầy đủ là gì?