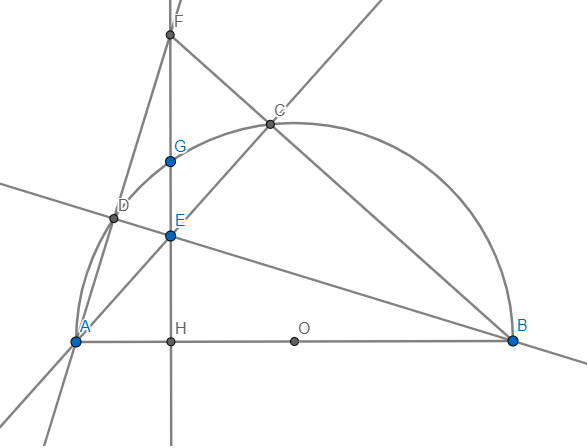
Cho đường tròn tâm O đường kính AB,trên cùng một nửa đường tròn (O) lấy 2 điểm G và E ( theo thứ tự A,G,E,B ) sao cho tia EG cắt tia BA tại D . Đường thẳng vuông góc với BD tại D cắt BE tại C , đường thẳng CA cắt đường tròn (O) tại điểm thứ 2 là F
a) Chứng minh tứ giác DFBC nội tiếp
b)Chứng minh BF=BG

a) Xét tam giác DFB có:
\(\hept{\begin{cases}\widehat{D}=90^o\left(DE\perp AB\right)\\\widehat{C}=90^o\end{cases}}\)
=> Tứ giác DFBC nội tiếp
b) Xét tam giác BFG có \(\hept{\begin{cases}\widehat{FBG}=\frac{1}{2}\widebat{AG}\\\widehat{BGF}=\frac{1}{2}\widebat{AE}\end{cases}}\)
Mà cung AB= cùng BG
=> BF=BG