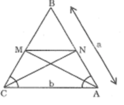
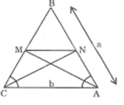
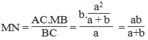cho tâm giác cân ABC có AB=BC đường phân giắc góc A cắt BC tại M đường phân giác góc C cắt BA tại N chứng minh MN//AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NH
5 tháng 4 2020
Vì △ABC có AB = BC (gt) => △ABC cân tại B => BAC = BCA => BAC : 2 = BCA : 2 => BAM = BCN
Xét △BAM và △BCN
Có: ABC là góc chung
AB = BC (gt)
BAM = BCN (cmt)
=> △BAM = △BCN (g.c.g)
=> BM = BN (2 cạnh tương ứng)
=> △BMN cân tại B
=> BNM = (180o - NBM) : 2
Vì △ABC cân tại B => BAC = (180o - ABC) : 2
=> BNM = BAC
Mà 2 góc này nằm ở vị trí so le trong
=> MN // AC (dhnb)
CM
31 tháng 12 2018
Trong △ BAC, ta có: AM là đường phân giác của (BAC)
Suy ra: 
(tỉnh chất đường phân giác) (1)
CN là đường phân giác của (BCA)
Suy ra: 
(tỉnh chất đường phân giác) (2)
Lại có: AB = CB = a (gt)
Từ (1), (2) và (gt) suy ra: 
Trong
△
BAC, ta có: 
Suy ra: MN // AC (theo định lí đảo của định lí Ta-lét).
CM
25 tháng 2 2017
Ta có: 
(chứng minh trên)
Suy ra:
Hay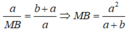 
Trong ΔBAC, ta có:
MN //AC (chứng minh trên)
Và 
Vậy 