cho phương trình \(3x^2+5x-6=0\) có 2 nghiệm phân biệt: x1;x2.Ko giải pt hãy lập pt bậc hai có các nghiệm : y1= x1+\(\frac{1}{x_2}\)và y2=x2+\(\frac{1}{x_1}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 3 2021
Theo hệ thức Vi-ét:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{5}{3}\left(1\right)\\x_1x_2=\dfrac{m}{3}\left(2\right)\end{matrix}\right.\)
Ta có \(6x_1+x_2=0\)\(\Rightarrow5x_1+\left(x_1+x_2\right)=0\Rightarrow5x_1+\dfrac{5}{3}=0\Leftrightarrow x_1=-\dfrac{1}{3}\) Thay vào (1) ta được:
\(x_2-\dfrac{1}{3}=\dfrac{5}{3}\Rightarrow x_2=2\)
Thay \(x_1=-\dfrac{1}{3};x_2=2\) vào (2) ta được:
\(-\dfrac{2}{3}=\dfrac{m}{3}\Rightarrow m=-2\)
HN
1 tháng 1 2022
Giải thích các bước giải:
a.Với m=6→x2−5x+6=0→(x−2)(x−3)=0→x∈{2,3}m=6→x2−5x+6=0→(x−2)(x−3)=0→x∈{2,3}
b.Để phương trình có 2 nghiệm x1,x2x1,x2
→Δ=52−4m≥0→m≤254→Δ=52−4m≥0→m≤254
→{x1+x2=5x1x2=m→{x1+x2=5x1x2=m
Mà |x1−x2|=3→(x1−x2)2=9|x1−x2|=3→(x1−x2)2=9
→(x1+x2)2−4x1x2=9→(x1+x2)2−4x1x2=9
→52−4m=9→52−4m=9
→m=−4
1 tháng 1 2022
a, khi m=6 thì pt\(\Leftrightarrow x^2-5x+6=0\)
\(\Leftrightarrow\left(x^2-2x\right)-\left(3x-6\right)=0\\ \Leftrightarrow x\left(x-2\right)-3\left(x-2\right)=0\\ \Leftrightarrow\left(x-2\right)\left(x-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\\x=3\end{matrix}\right.\)
b,Ta có:\(\Delta=\left(-5\right)^2-4.1.m=25-4m\)
để pt có 2 nghiệm x1, x2 phân biệt thì \(\Delta>0\) hay \(25-4m>0\Rightarrow m< \dfrac{25}{4}\)
25 tháng 5 2022
\(\Delta=\left(-5\right)^2-4\left(m-1\right)\)
\(=25-4m+4\)
\(=29-4m\)
Để pt có 2 nghiệm thì \(\Delta>0\)
\(\Leftrightarrow m< \dfrac{29}{4}\)
Theo hệ thức Vi-ét, ta có: \(\left\{{}\begin{matrix}x_1+x_2=5\\x_1x_2=m-1\end{matrix}\right.\) (1)
\(2x_2=\sqrt{x_1}\) ; \(ĐK:x_1;x_2\ge0\)
\(\Leftrightarrow4x_2^2=\left|x_1\right|\)
\(\Leftrightarrow4x_2^2=x_1\) (2)
Thế \(x_1=4x^2_2\) vào \(\left(1\right)\), ta được:
\(\left\{{}\begin{matrix}4x_2^2+x_2-5=0\\4x_2^3-m+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x_2=-\dfrac{5}{4}\left(ktm\right)\\x_2=1\left(tm\right)\end{matrix}\right.\\4.1^3-m+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_2=1\\m=5\end{matrix}\right.\)
\(\left(2\right)\Rightarrow x_1=4\)
Vậy \(\left\{{}\begin{matrix}m=5\\x_1=4\\x_2=1\end{matrix}\right.\)
CM
9 tháng 3 2019
x 2 - 3x + m - 5 = 0
a = 1; b = -3; c = m – 5
Δ = b 2 - 4ac = - 3 2 - 4(m - 5) = 29 - 4m
Phương trình có 2 nghiệm phân biệt x 1 ; x 2 khi và chỉ khi
Δ > 0 ⇔ 29 - 4m > 0 ⇔ m < 29/4
Theo định lí Vi-et ta có:
x 1 ; x 2 = c/a = m - 5
Theo bài ra
x 1 ; x 2 = 4 ⇔ m - 5 = 4 ⇔ m = 9 (Không TMĐK m < 29/4)
Vậy không tồn tại m thỏa mãn đề bài.
30 tháng 6 2020
a, \(x^2-3x-6+4=0\)
\(\Leftrightarrow x^2-3x-2=0\)
Ta có : \(\left(-3\right)^2-4.\left(-2\right)=9+8=17>0\)
Nên có 2 nghiệm phân biệt
\(x_1=\frac{3-\sqrt{17}}{2};x_2=\frac{3+\sqrt{17}}{2}\)
b, Để PT có nghiệm thì \(\Delta=0\)
\(\Leftrightarrow b^2-4ac=0\)
\(\Leftrightarrow\left(-3\right)^2-4\left(-m+4\right)=0\)
\(\Leftrightarrow9+4m-16=0\)
\(\Leftrightarrow7+4m=0\)
\(\Leftrightarrow m=-\frac{7}{4}\)
Vậy => m = -7/4
c, Ko rõ
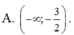
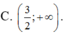
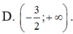
Lời giải:
Áp dụng định lý Vi-et cho 2 nghiệm $x_1,x_2$ của pt $3x^2+5x-6=0$ ta có:
\(\left\{\begin{matrix} x_1+x_2=\frac{-5}{3}\\ x_1x_2=-2\end{matrix}\right.\)
Khi đó:
\(\left\{\begin{matrix} y_1+y_2=x_1+\frac{1}{x_2}+x_2+\frac{1}{x_1}=(x_1+x_2)+\frac{x_1+x_2}{x_1x_2}=\frac{-5}{3}+\frac{-5}{3.(-2)}=\frac{-5}{6}\\ y_1y_2=x_1x_2+1+1+\frac{1}{x_1x_2}=-2+2+\frac{1}{-2}=\frac{-1}{2}\end{matrix}\right.\)
Áp dụng định lý Vi-et đảo, $y_1,y_2$ là nghiệm của pt:
$y^2+\frac{5}{6}y-\frac{1}{2}=0$
$\Leftrightarrow 6y^2+5y-3=0$ (đây là pt cần tìm)