Cho hàm số y = f(x) = mx + 2m − 3 có đồ thị (d). gọi A, B là hai điểm thuộc đồ thị
và có hoành độ lần lượt là −1 và 2.
1 Xác định tọa độ hai điểm A và B.
2 Tìm m để cả hai điểm A và B cùng nằm phía trên trục hoành.
3 Tìm điều kiện của m để f(x) > 0, ∀x ∈ [−1; 2]
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: 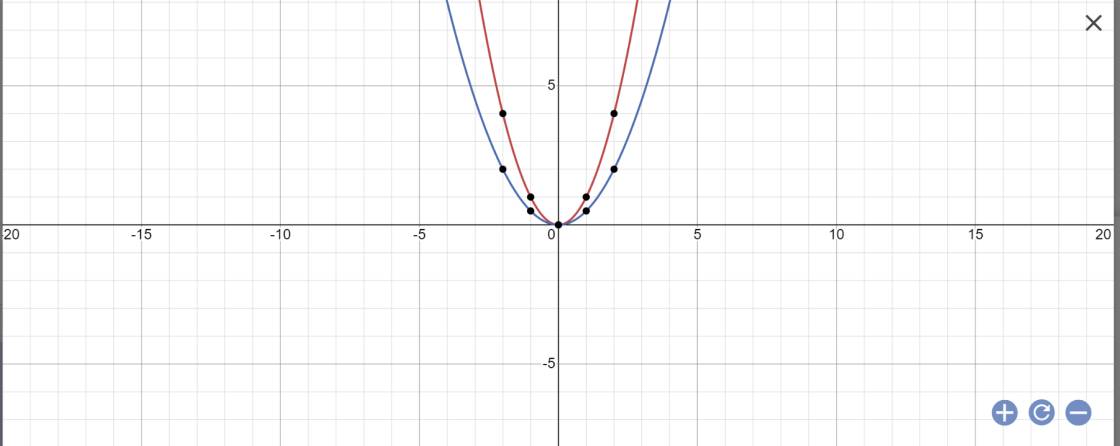
b: Khi x=2 thì y=1/2*2^2=2
=>A(2;2)
Khi x=2 thì y=2^2=4
=>B(2;4)
c: Tọa độ A' là:
\(\left\{{}\begin{matrix}x_{A'}=-x_A=-2\\y_{A'}=y_A=2\end{matrix}\right.\)
Vì f(-2)=1/2*(-2)^2=2
nên A' thuộc (P1)
Tọa độ B' là:
\(\left\{{}\begin{matrix}x_{B'}=-x_B=-2\\y_{B'}=y_B=4\end{matrix}\right.\)
Vì f1(-2)=(-2)^2=4
nên B' thuộc y=x^2

e ơi, mình trình bày giấy thì viết rõ ràng xíu để mng đọc dc nha

\(a)\)Vì đths \(y=\left(2m-\frac{1}{2}\right)x\)đi qua \(A\left(-2;5\right)\)
\(\Rightarrow\)Thay \(x=-2;y=5\)vào hàm số
\(\Leftrightarrow\left(2m-\frac{1}{2}\right)\left(-2\right)=5\)
\(\Leftrightarrow2m-\frac{1}{2}=-\frac{5}{2}\)
\(\Leftrightarrow2m=-2\)
\(\Leftrightarrow m=-1\)
\(b)m=-1\)
\(\Leftrightarrow y=-\frac{5}{2}x\)
\(c)\)Lập bảng giá trị:
| \(x\) | \(0\) | \(-2\) |
| \(y=-\frac{5}{2}x\) | \(0\) | \(5\) |
\(\Rightarrow\)Đths \(y=-\frac{5}{2}x\)là một đường thẳng đi qua hai điểm \(O\left(0;0\right);\left(-2;5\right)\)
Tự vẽ :<
\(d)\)Chỉ cần thành hoành độ hoặc tung độ là x hoặc y vào đths trên là tìm được cái còn lại. Khi đó tìm được tọa độ của 2 diểm trên.

Bài 3:
Đặt \(a=m^2-4\)
\(a)\) Đồ thị hàm số \(y=\left(m^2-4\right)x-5\)nghịch biến
\(\Leftrightarrow a< 0\)
\(\Leftrightarrow m^2-4< 0\)
\(\Leftrightarrow m^2< 4\)
\(\Leftrightarrow-\sqrt{4}< m< \sqrt{4}\)
\(\Leftrightarrow-2< m< 2\)
Vậy với \(-2< m< 2\)thì hàm số nghịch biến
\(b)\) Đồ thị hàm số \(y=\left(m^2-4\right)x-5\)đồng biến \(\forall x>0\)
\(\Leftrightarrow a>0\)
\(\Leftrightarrow m^2-4>0\)
\(\Leftrightarrow m^2>4\)
\(\Leftrightarrow\orbr{\begin{cases}m>2\\m< -2\end{cases}}\)
Vậy với \(\orbr{\begin{cases}m>2\\m< -2\end{cases}}\)thì hàm số đồng biến \(\forall x>0\)
