Giải giúp em câu bcdef với ạ riêng b,e,f giải đưa về cos giúp em
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


e:
\(E=\left(\dfrac{\sqrt{15}-\sqrt{20}}{2-\sqrt{3}}+\dfrac{\sqrt{21}-\sqrt{7}}{1-\sqrt{3}}\right):\dfrac{1}{\sqrt{7}-\sqrt{5}}\)
\(=\left(-\dfrac{\sqrt{5}\left(2-\sqrt{3}\right)}{2-\sqrt{3}}-\dfrac{\sqrt{7}\left(1-\sqrt{3}\right)}{1-\sqrt{3}}\right)\cdot\dfrac{\sqrt{7}-\sqrt{5}}{1}\)
\(=-\left(\sqrt{7}+\sqrt{5}\right)\left(\sqrt{7}-\sqrt{5}\right)\)
=-2
f: \(F=\sqrt{3}+1+2-\sqrt{3}=3\)

j, ĐK: \(x\ne\dfrac{\pi}{6}+\dfrac{k\pi}{2}\)
\(tan\left(\dfrac{\pi}{3}+x\right)-tan\left(\dfrac{\pi}{6}+2x\right)=0\)
\(\Leftrightarrow tan\left(\dfrac{\pi}{3}+x\right)=tan\left(\dfrac{\pi}{6}+2x\right)\)
\(\Leftrightarrow\dfrac{\pi}{3}+x=\dfrac{\pi}{6}+2x+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{6}+k\pi\left(l\right)\)
\(\Rightarrow\) vô nghiệm.

a)
4Na + O2 ---to→ 2Na2O
Na2O + H2O → 2NaOH
2NaOH + CO2 → Na2CO3 + H2O
Na2CO3 + Ca(OH)2 → 2NaOH + CaCO3
CaCO3 ---to→ CaO + CO2
CO2 + NaOH → NaHCO3
NaHCO3 + H2SO4 → Na2SO4 + CO2 + H2O
Na2SO4 + Ba(OH)2 → 2NaOH + BaSO4
b)
S + O2 ---to→ SO2
2SO2 + O2 ---to(V2O5)→ 2SO3
SO3 + H2O → H2SO4
H2SO4 + Cu(OH)2 → CuSO4 + 2H2O
CuSO4 + FeCl2 → CuCl2 + FeSO4
FeSO4 + 2NaOH → Fe(OH)2 + Na2SO4
Fe(OH)2 + 2HCl → FeCl2 + 2H2O
2FeCl2 + Cl2 → 2FeCl3
2FeCl3 + 3Ba(OH)2 → 2Fe(OH)3 + 3BaCl2
2Fe(OH)3 ---to→ Fe2O3 + 3H2O
Fe2O3 + 3H2SO4 → Fe2(SO4)3 + 3H2O

b: Tọa độ giao là:
5x-4=2x+2 và y=2x+2
=>x=2 và y=6
c: Vì (d2)//d nên (d2): y=2x+b
Thay x=1 và y=3 vào (d2), ta được:
b+2=3
=>b=1


Người mẹ trằn trọc không phải vì quá lo lắng cho con mà là vì đang sống lại với những kỉ niệm xưa của chính mình. Ngày khai trường của đứa con đã làm sống dậy trong lòng người mẹ một ấn tượng thật sâu đậm từ ngày còn nhỏ, khi cũng như đứa con bây giờ, lần đầu tiên được mẹ (tức bà ngoại của em bé bây giờ) đưa đến trường. Cảm giác chơi vơi hốt hoảng khi nhìn người mẹ đứng ngoài cánh cổng trường đã khép còn in sâu mãi cho đến tận bây giờ.
Tấm lòng của người mẹ rất cao cả và thiêng liêng.Mẹ rất lo cho con

Lời giải:
$\frac{x-2y}{3z}$ có thể nhận giá trị lớn nhất nếu $x$ lớn nhất và $y,z$ nhỏ nhất có thể.
$x$ lớn nhất có thể nhận là $14$ (theo điều kiện)
$y,z$ nhỏ nhất có thể nhận là $1,2$ (do $y,z$ phân biệt)
Nếu $x=14, y=1,z=2$ thì $\frac{x-2y}{3z}=2$
Nếu $x=14; y=2, z=1$ thì $\frac{x-2y}{3z}=\frac{10}{3}>2$
Đáp án D.

cái này áp dụng hệ thức lượng thôi bạn
AH=căn 6^2-4,8^2=3,6cm
=>AC=6^2/3,6=10cm




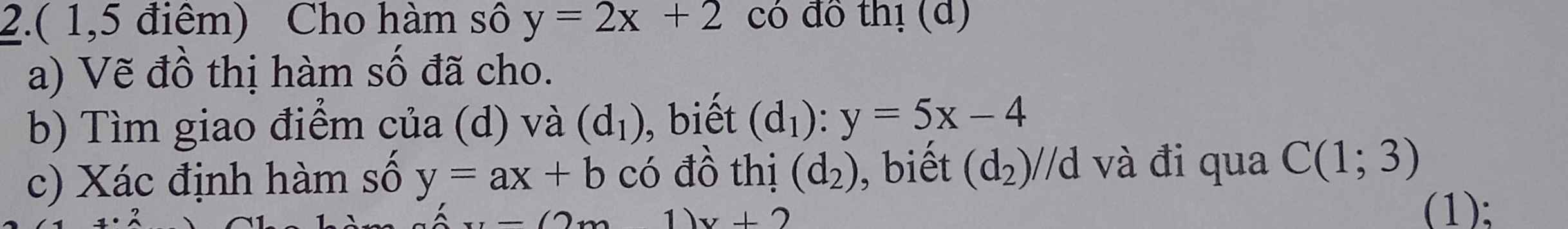





b.
\(\Leftrightarrow\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx=-\dfrac{1}{2}\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{3}\right)=-\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{3}=\dfrac{2\pi}{3}+k2\pi\\x+\dfrac{\pi}{3}=-\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k2\pi\\x=-\pi+k2\pi\end{matrix}\right.\)
c.
\(\Leftrightarrow\dfrac{3}{5}sinx-\dfrac{4}{5}cosx=1\)
Đặt \(\dfrac{3}{5}=cosa\) với \(a\in\left(0;\dfrac{\pi}{2}\right)\Rightarrow\dfrac{4}{5}=sina\)
Pt trở thành:
\(sinx.cosa-cosx.sina=1\)
\(\Leftrightarrow sin\left(x-a\right)=1\)
\(\Leftrightarrow x-a=\dfrac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=a+\dfrac{\pi}{2}+k2\pi\)