cho \(A=\dfrac{a^3}{24}+\dfrac{a^2}{8}+\dfrac{a}{12}\)với a là số tự nhiên. Chứng tỏ A∈Z
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VA
27 tháng 4 2023
Với a,b,c dương, ta có:
a/a+b > a/a+b+c
b/b+c > b/a+b+c
c/c+a > c/a+b+c
=> A > a/a+b+c + b/a+b+c + c/a+b+c => A>1. (1)
Ta lại có
A = a/a+b + b/b+c + c/c+a
= a+b-b/a+b + b+c-c/b+c + c+a-a/c+a
= 1-b/a+b + 1-c/b+c + 1-a/c+a
= 3-(b/a+b + c/b+c + a/c+a) = 3-B
Tương tự phần chứng minh trên, ta có
b/a+b > b/a+b+c
c/b+c > c/a+b+c
a/a+c > a/a+b+c
=> B > b/a+b+c + c/a+b+c + a/a+b+c => B>1
mà A = 3-B
=> A < 2 (2)
Từ (1) và (2) => 1<A<2
Mà không có số tự nhiên nào ở giữa 1 và 2 => A không là số tự nhiên
MH
19 tháng 4 2022
a) \(2\left(\dfrac{2}{3.5}+\dfrac{4}{5.9}+...+\dfrac{16}{n\left(n+16\right)}\right)=\dfrac{16}{25}\)
\(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{9}+...+\dfrac{1}{n}-\dfrac{1}{n+16}=\dfrac{8}{25}\)
\(\dfrac{1}{3}-\dfrac{1}{n+16}=\dfrac{8}{25}\)
\(\dfrac{n+13}{3\left(n+16\right)}=\dfrac{8}{25}\)
\(24n+384=25n+325\)
\(25n-24n=384-325\)
\(n=59\)
26 tháng 3 2021
Bài 2:
a) Ta có: \(A=\dfrac{4}{n-1}+\dfrac{6}{n-1}-\dfrac{3}{n-1}\)
\(=\dfrac{4+6-3}{n-1}\)
\(=\dfrac{7}{n-1}\)
Để A là số tự nhiên thì \(7⋮n-1\)
\(\Leftrightarrow n-1\inƯ\left(7\right)\)
\(\Leftrightarrow n-1\in\left\{1;7\right\}\)
hay \(n\in\left\{2;8\right\}\)
Vậy: \(n\in\left\{2;8\right\}\)
27 tháng 3 2021
ta có B=2n+9/n+2-3n+5n+1/n+2=4n+10/n+2 Để B là STN thì 4n+10⋮n+2 4n+8+2⋮n+2 4n+8⋮n+2 ⇒2⋮n+2 n+2∈Ư(2) Ư(2)={1;2} Vậy n=0
HH
1
AH
Akai Haruma
Giáo viên
20 tháng 1 2018
Lời giải:
Ta có: \(A=\frac{a}{3}+\frac{a^2}{2}+\frac{a^3}{6}\)
\(\Leftrightarrow A=\frac{2a+3a^2+a^3}{6}\)
Xét tử số:
\(a^3+3a^2+2a=a(a^2+3a+2)\)
\(=a[a(a+2)+(a+2)]\)
\(=a(a+1)(a+2)\)
Vì $a,a+1$ là hai số nguyên liên tiếp nên
\(a(a+1)\vdots 2\Rightarrow a(a+1)(a+2)\vdots 2\)
\(\Leftrightarrow a^3+3a^2+2a\vdots 2\) (1)
Mặt khác \(a,a+1,a+2\) là ba số nguyên liên tiếp nên tích của chúng chia hết cho $3$
\(\Leftrightarrow a(a+1)(a+2)\vdots 3\)
\(\Leftrightarrow a^3+3a^2+2a\vdots 3\) (2)
Từ (1)(2) kết hợp với $(2,3)$ nguyên tố cùng nhau suy ra \(a^3+3a^2+2a\vdots 6\)
\(\Rightarrow A=\frac{a^3+3a^2+2a}{6}\in\mathbb{Z}\). Ta có đpcm.
7 tháng 3 2021
A=1/2+1/3+..+1/2019 < 1>
A= 1+1/2+1/3+..+1/2019 < 1>
A=1+1/2+1/3+..+1/2019 <1>
A=1+1/2+1/3+..+1/2019 <2018>
Vì 2018/2019 <1>
nên A=1/2+1/3+..+1/2019<1>
=> A=1/2+1/3+..+1/2019 không phải là số tự nhiên.
AH
Akai Haruma
Giáo viên
8 tháng 3 2021
Mình chưa hiểu cách bạn làm với dấu <1> cho lắm.
Theo mình hiểu thì bạn đang chứng minh $A< 1$ nên $A$ không phải số tự nhiên. Mà điều này thì sai vì $A=1+(\frac{1}{2}+\frac{1}{3}+...)$ hiển nhiên lớn hơn $1$.
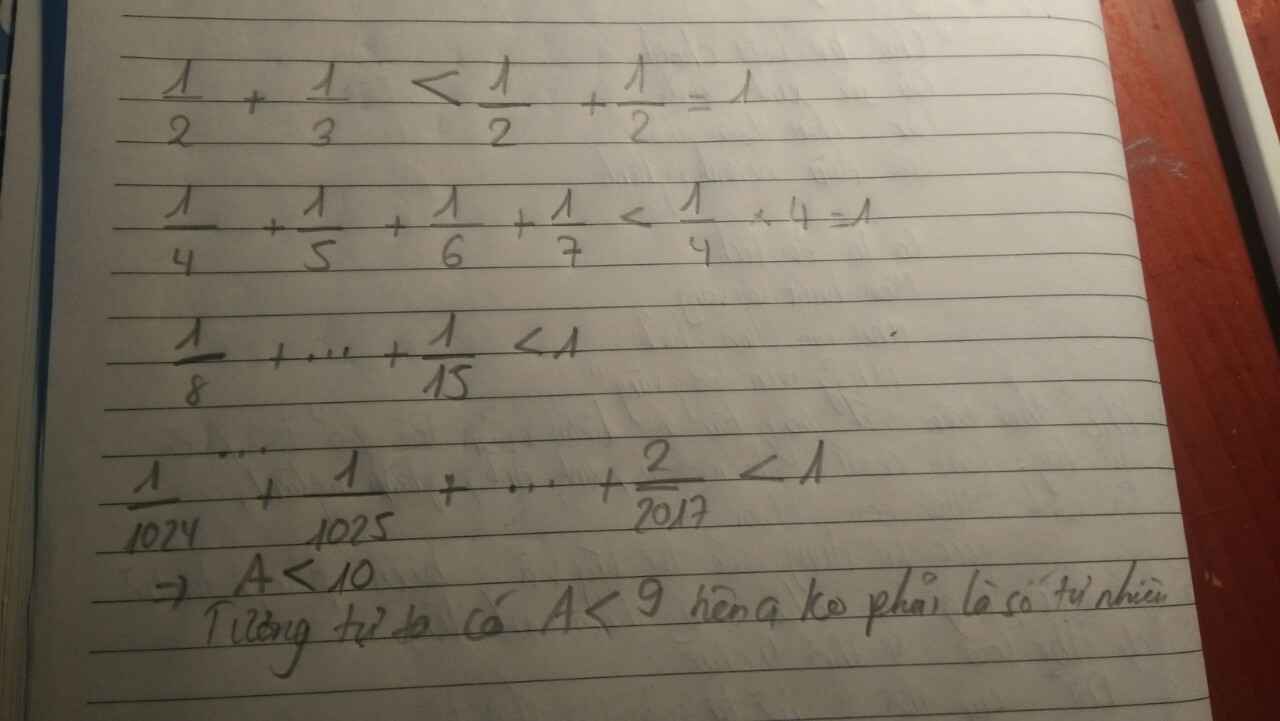
Đề bài không đúng, A chỉ nhận giá trị nguyên khi a chẵn, còn a lẻ thì A là phân số không nguyên