Nhìn hình chứng minh:
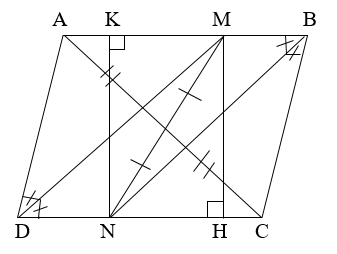
a) Chứng minh AM = CN.
b) Chứng minh tứ giác DMBN là hình bình hành.
c) Gọi H, K lần lượt là hình chiếu của M và N trên BN và DM. Chứng minh hai đoạn thẳng AC và MN cắt nhau tại trung điểm mỗi đường.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 10 2021
a: Xét ΔADM và ΔCBN có
\(\widehat{ADM}=\widehat{CBN}\)
AD=CB
\(\widehat{A}=\widehat{C}\)
Do đó: ΔADM=ΔCBN
Suy ra: AM=CN
19 tháng 10 2021
a: Xét ΔADM và ΔCBN có
\(\widehat{ADM}=\widehat{CBN}\)
AD=CB
\(\widehat{A}=\widehat{C}\)
Do đó: ΔADM=ΔCBN
Suy ra: AM=CN
22 tháng 9 2023
a: ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
mà O là trung điểm của AC
nên O là trung điểm của BD
Xét ΔMDO và ΔBNO có
\(\widehat{MDO}=\widehat{NBO}\)
OD=OB
\(\widehat{MOD}=\widehat{NOB}\)
Do đó: ΔMDO=ΔBNO
=>MD=BN
b: Xét tứ giác DMBN có
DM//BN
DM=BN
Do đó: DMBN là hình bình hành
c; DMBN là hình bình hành
=>DB cắt MN tại trung điểm của mỗi đường
mà O là trung điểm của BD
nên O là trung điểm của MN
25 tháng 10 2018
cccccccccccccccccccccccccccccccuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuutttttttttttttttttttttttttttttttttttt