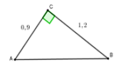
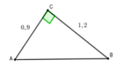
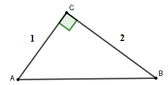
Cho tam giác ABC vuông tại C có AC = 1 , BC =2 .Tính các tỉ số lượng giác sinB , Cos B
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
15 tháng 7 2017
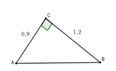
Theo định lý Py-ta-go ta có:
Xét tam giác ABC vuông tại C có:
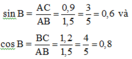
Đáp án cần chọn là: A
TH
1
AP
26 tháng 11 2021
Xét \(\Delta ABC\) vg tại A có
BC\(^2\)= AC\(^2\)+AB\(^2\)( theo định lí Pi ta go)
\(\Rightarrow\)AB\(^2\)=BC\(^2\)-AC\(^2\)\(\Leftrightarrow\)AB\(^2\)=1,2\(^2\)-0,9\(^2\)=1,44 - 0,81= 0,63
\(\Rightarrow\)AB=\(\sqrt{0,63}\)=\(\dfrac{3\sqrt{7}}{10}\)
\(\Rightarrow\)sin B=\(\dfrac{AC}{BC}=\dfrac{0,9}{1,2}=\dfrac{3}{4}\)
sinC=\(\dfrac{AB}{BC}=\)\(\dfrac{\dfrac{3\sqrt{7}}{10}}{1,2}\)=\(\dfrac{\sqrt{7}}{4}\)
CM
18 tháng 8 2018
Theo định lý Py-ta-go:
Xét tam giác ABC vuông tại C có:
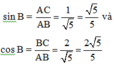
Đáp án cần chọn là: B
16 tháng 8 2020
\(\sin\alpha=\frac{2}{5}\)
\(\Rightarrow\cos\alpha=\sqrt{1-\sin^2\alpha}\)
\(=\sqrt{1-\frac{4}{25}}\)
\(=\sqrt{\frac{21}{25}}=\)\(\frac{\sqrt{21}}{5}\)
\(\Rightarrow\tan\alpha=\frac{\sin\alpha}{\cos\alpha}=\frac{2}{5}:\frac{\sqrt{21}}{5}=\frac{2}{\sqrt{21}}\)và \(\cot\alpha=\frac{\sqrt{21}}{2}\)
2. Tương tự a)
\(\cos B=\sqrt{1-\sin^2B}\)
\(=\sqrt{1-\frac{1}{4}}\)
\(=\sqrt{\frac{3}{4}}=\frac{\sqrt{3}}{2}\)
\(\tan B,\cot B\)bạn tự tính nốt.
PD
16 tháng 8 2020
\(sin\alpha=0,4\Rightarrow sin^2\alpha=0,16\Rightarrow cos^2\alpha=1-sin^2\alpha=1-0,16=0,84\Rightarrow cos\alpha=\frac{\sqrt{21}}{5}\)
\(tan\alpha=\frac{sin\alpha}{cos\alpha}=\frac{0,4}{\frac{\sqrt{21}}{5}}=\frac{2\sqrt{21}}{21}\)
\(cot\alpha=1:sin\alpha=1:\frac{2\sqrt{21}}{21}=\frac{21}{2\sqrt{21}}\)
NA
0
SD
0
CD
0