Bài 1: Cho tam giác ABC có MN//BC và AM/AB=1/2,MN =3cm. Tính BC
Bài 2: Cho hình thang ABCD(AB//CD); hai đường chéo cắt nhau tại O. Qua O kẻ đường thẳng song song với AB cắt AD lần lượt tại M và N (hình 31). Chứng minh OM=ON.
Bài 3: Trên các cạnh của AB, AC của ∆ABClần lượt lấy điểm M và N sao cho AM/MB=AN/NC. Gọi I là trung điểm của BC, K là giao điểm của AI và MN. Chứng minh KM=KN
Bài 4: Cho hình vuông ABCD cạnh 6cm. Trên tia đối của AD lấy điểm I sao cho AI=2cm. IC cắt AB tại K. Tính độ dài IK và IC
các bạn giúp mình với vì chiều nay nộp bài r nên mình gấp lắm ạ😫😫😫

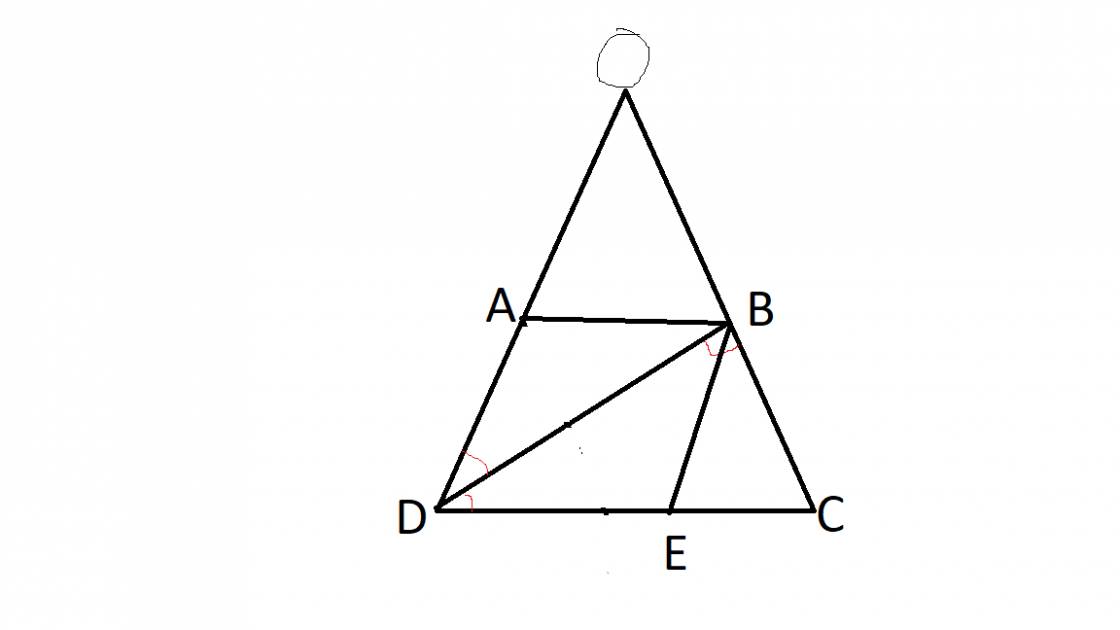
Vì MN//BC, theo hệ quả của định lí Ta-let, ta có:
\(\frac{AM}{AB}=\frac{MN}{BC}\) hay \(\frac{1}{2}=\frac{3}{BC}\)
⇒ \(BC=2.3=6(cm)\)
Bài 2:
Vì MN//AB, theo hệ quả của định lí Ta-let ta có:
\(\frac{OM}{AB}=\frac{DO}{DB}\) (1)
\(\frac{ON}{AB}=\frac{CO}{CA}\) (2)
Theo định lí Ta-let:
\(\frac{DO}{OB}=\frac{CO}{OA}\) ⇒ \(\frac{DO}{OB}=\frac{CO}{CA}\left(3\right)\)
Từ(1),(2),(3)⇒\(\frac{OM}{AB}=\frac{ON}{AB}\) ⇒ OM=ON(đpcm)
Bài 3:
Ta có:\(\frac{AM}{AB}=\frac{AN}{NC}\) ⇒ MN//BC
Vì MN//BC, theo hệ quả của định lí Ta-let, ta có:
\(\frac{MK}{BI}=\frac{AK}{AI}\) (1)
\(\frac{NK}{CI}=\frac{AK}{AI}\left(2\right)\)
Từ (1),(2)⇒\(\frac{MK}{BI}=\frac{NK}{CI}\) (3)
Mà I là trung điểm của BC⇒BI=CI(4)
Từ (3),(4)⇒MK=NK(đpcm)
Bài 4:
Vì AK//CD, theo hệ quả của định lí Ta-let ta có:
\(\frac{IA}{ID}=\frac{IK}{IC}hay\frac{2}{8}=\frac{IK}{IC}\)
⇒ IK=2cm, IC=8cm
Cho góc xAy khác góc bẹt. Trên tia Ax lấy các điểm B, C. Qua B và C vẽ hai đường thẳng song song cắt Ay lần lượt ở D và E. Qua E vẽ đường thẳng song song với CD cắt tia Ax ở F
a)so sánh AB/AC và AD/AE; AC/AF và AD/AE
b)CM: rằng AC bình phương = AB.AF