Cho tam giác ABC cân tại A. Kẻ BD vuông góc với đường thẳng AC tại D. Lấy điểm E bất kì trên cạnh BC (E khác B, khác C). Kẻ EF, EG, EH lần lượt vuông góc với AB, AC, BD.1. Chứng minh rằng tam giác HBE bằng tam giác FEB.2. Chứng minh rằng EF + EG = BD.3. Trên tia đối của tia CA lấy điểm K sao KC = BF ; BC cắt FK tại I. Chứng minh rằng I là trung điểm của FK.4. Nêu cách xác định điểm E trên BC để tam giác...
Đọc tiếp
Cho tam giác ABC cân tại A. Kẻ BD vuông góc với đường thẳng AC tại D. Lấy điểm E bất kì trên cạnh BC (E khác B, khác C). Kẻ EF, EG, EH lần lượt vuông góc với AB, AC, BD.
1. Chứng minh rằng tam giác HBE bằng tam giác FEB.
2. Chứng minh rằng EF + EG = BD.
3. Trên tia đối của tia CA lấy điểm K sao KC = BF ; BC cắt FK tại I. Chứng minh rằng I là trung điểm của FK.
4. Nêu cách xác định điểm E trên BC để tam giác EGH vuông cân.
giải gấp nhé cảm ơn trước
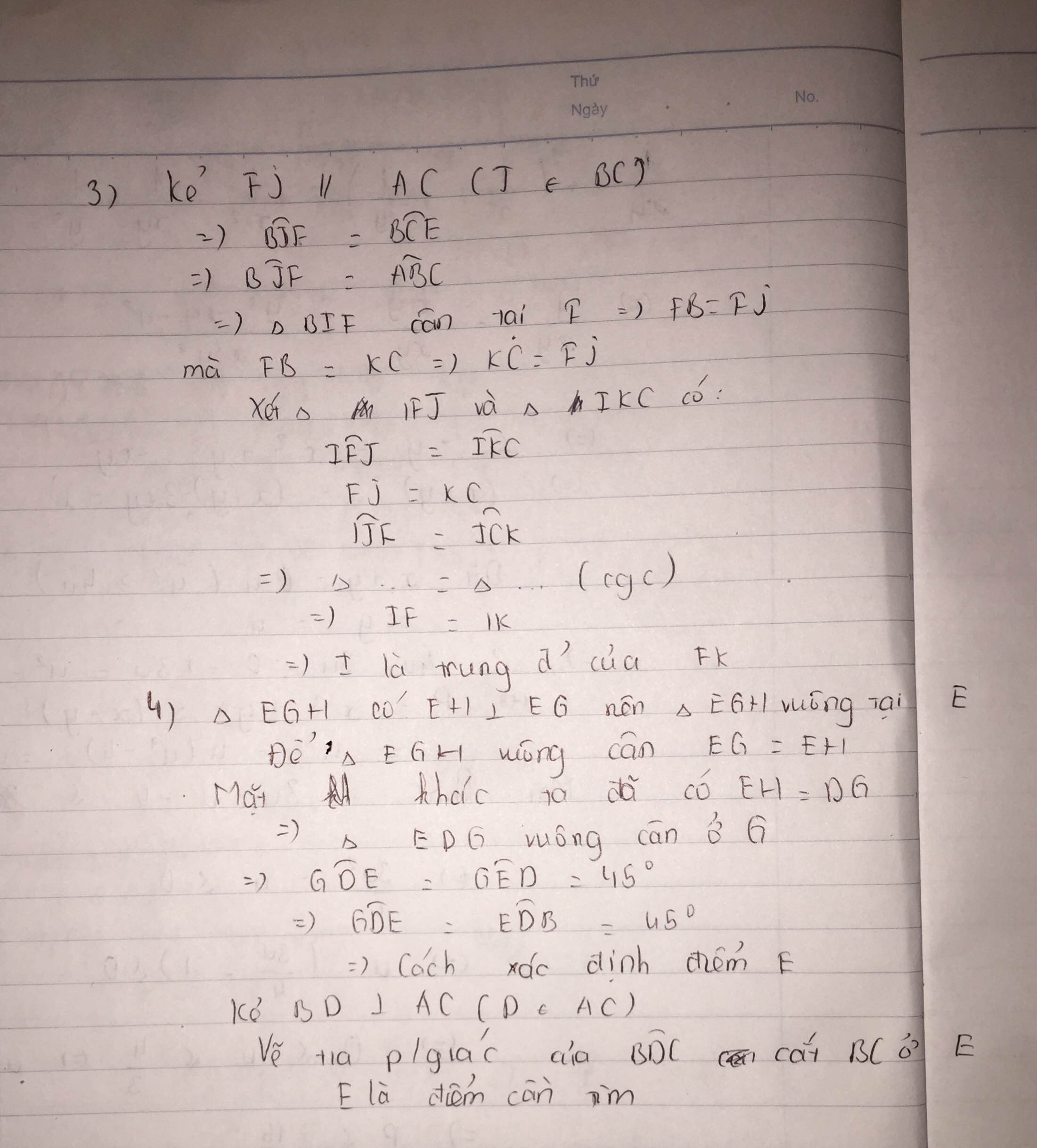
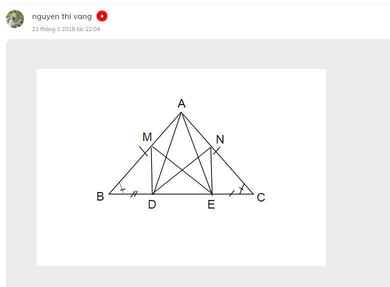
a, EH _|_ BD (GT)
CD _|_ BD (GT)
=> CD // EH (tc)
=> góc HEB = góc ACB (đồng vj)
góc ACB = góc ABC do tam giác ABC cân tại A (gt)
=> góc HEB = góc ABC
xét tam giác BFE và tam giác EHB có : BE chung
góc BFE = góc EHB = 90
=> tam giác BFE = tam giác EHB (ch-gn)
b, tam giác BFE = tam giác EHB (câu a)
=> EF = BH (đn) (1)
xét tứ giác HDGE có góc EHD = góc HDG = góc DGE = 90
=> HDGE là hình chữ nhật (dh )
=> HD = EG
BH + HD = BD và (1)
=> EF + EG = BD
c,