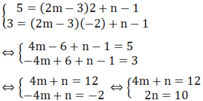Cho (d) mx-y=2m
(d') x-my = m+1
Tìm m để (d) cắt (d') tại điểm
a) Cách đều 2 trục tọa độ
b) Thuộc tia phân giác góc phần tư thứ 1
c) Thuộc đường thẳng x-3y = 5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
+ Tọa độ giao điểm của hai đường thẳng d và d’ là nghiệm của hệ phương trình:
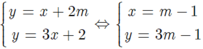
suy ra d và d’ cắt nhau tại M( m-1; 3m-1)
+ Vì ba đường thẳng d; d’ ; d’’ đồng quy nên d’’ qua M ta có
3m-1= -m( m-1) + 2 hay m2+ 2m-3=0
Suy ra m=1 hoặc m= -3
Với m= 1 ta có ba đường thẳng là d: y= x+ 2; d’ : y= 3x+ 2 và d’’: y= -x+ 2 phân biệt và đồng quy tại M(0; 2).
Với m= -3 ta có d và d’’ trùng nhau suy ra m= -3 không thỏa mãn
Vậy m= 1 là giá trị cần tìm.
Chọn B.

xét hoành độ giao điểm của (d) và (p)
ta có : \(\dfrac{-x^2}{4}=mx-2m-1\Leftrightarrow\dfrac{x^2}{4}+mx-2m-1=0\)
\(\Leftrightarrow x^2+4mx-8m-4=0\)
\(\Delta'=\left(2m\right)^2-\left(-8m-4\right)=4m^2+8m+4=\left(2m+2\right)^2\ge0\)
\(\Rightarrow\) (d) tiếp súc hoặc cắt (p)
TH1 : (d) tiếp xúc (p) \(\Leftrightarrow\) phương trình có nghiệm kép
ta có : \(\left(2m+2\right)^2=0\Leftrightarrow2m+2=0\Leftrightarrow2m=-2\Leftrightarrow m=-1\)
\(x_1=x_2=\dfrac{-b'}{a}=\dfrac{-2m}{1}=-2m=-2\left(-1\right)=2\)
\(x=2\Rightarrow y=\dfrac{-2^2}{4}=\dfrac{-4}{4}=-1\) vậy (d) tiếp xúc với (p) tại A\(\left(2;-1\right)\)
TH2 : (d) cắt (p) tại 2 điểm phân biệt \(\Leftrightarrow\) phương trình có nghiệm kép
\(\Leftrightarrow\) \(\left(2m+2\right)^2>0\Leftrightarrow2m+2\ne0\Leftrightarrow2m\ne-2\Leftrightarrow m\ne-1\)
th1: \(2m+2\ge0\Leftrightarrow2m\ge-2\Leftrightarrow m\ge-1\)
\(x_1=\dfrac{-2m+2m+2}{1}=2\Rightarrow y_1=\dfrac{-2^2}{4}=-1\) \(B\left(2;-1\right)\)
\(x_2=\dfrac{-2m-2m-2}{1}-4m-2\Rightarrow y_2=\dfrac{-\left(-4m-2\right)^2}{4}=\dfrac{-16m^2-8m-4}{4}=-4m^2-2m-1\)C\(\left(-4m-2;-4m^2-2m-1\right)\)
th2: \(2m+2< 0\Leftrightarrow2m< -2\Leftrightarrow m< -1\)
\(x_1=\dfrac{-2m+2+2m}{1}=2\Rightarrow y_1=\dfrac{-2^2}{4}=-1\)
D\(\left(2;-1\right)\) \(x_2=\dfrac{-2m-2m-2}{1}-4m-2\Rightarrow y_2=\dfrac{-\left(-4m-2\right)^2}{4}=\dfrac{-16m^2-8m-4}{4}=-4m^2-2m-1\)F\(\left(-4m-2;-4m^2-2m-1\right)\) vậy \(\Rightarrow\) kết luận ...................................................................................

Có đường thẳng d : y=mx-2m-1 đi qua gốc O
<=> đường thẳng d : y=mx-2m-1 đi qua điểm (0,0)
<=> 0 = 0.m-2.m-1
<=> 0 = -2.m-1
<=> -2m = 1
<=> m = \(\dfrac{-1}{2}\) (thỏa mãn điều kiện m ≠ 0)
Vậy m = \(\dfrac{-1}{2}\) để đường thẳng d : y=mx-2m-1 đi qua gốc O

Thay x=1 và y=-1 vào (d), ta được:
\(m-2m+1+3=0\)
hay m=4