Cho góc vuông xOy. Các điểm A, B theo thứ tự di chuyển trên Ox và Oy sao cho OA + OB = k (k là hằng số). Vẽ đường tròn (A; OB) và (B; OA). C/minh hai đường tròn (A) và (B) luôn luôn cắt nhau.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 8 2017
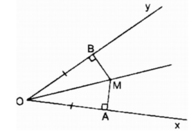
Xét hai tam giác vuông MOA và MOB: ∠ (MAO) = ∠ (MBO) = 90 0
OA = OB (gt)
OM cạnh huyền chung
Do đó: ∆ MAO = ∆ MBO (cạnh huyền, cạnh góc vuông)
⇒ ∠ (AOM) = ∠ (BOM)
A và B thay đổi, OA và OB luôn bằng nhau nên ∆ MAO và ∆ MBO luôn luôn bằng nhau do đó ∠ (AOM) = ∠ (BOM)
Vậy khi A chuyển động trên Ox, B chuyển động trên Oy mà OA = OB thì điểm M chuyển động trên tia phân giác của góc xOy.
TP
28 tháng 1 2018
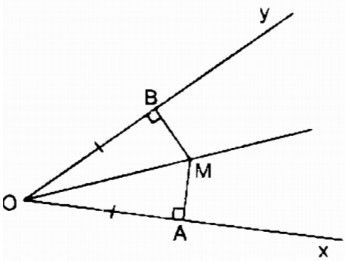
Xét hai tam giác vuông MOA và MOB:
\(\widehat{MAO}=\widehat{MBO}=90^0\)
OA = OB (gt)
OM cạnh huyền chung
Do đó: ∆ MAO = ∆ MBO (cạnh huyền, cạnh góc vuông)
⇒\(\widehat{AOM}=\widehat{BOM}\)
A và B thay đổi, OA và OB luôn bằng nhau nên ∆ MAO và ∆ MBO luôn luôn bằng nhau do đó \(\widehat{AOM}=\widehat{BOM}\)
Vậy khi A chuyển động trên Ox, B chuyển động trên Oy mà OA = OB thì điểm M chuyển động trên tia phân giác của góc xOy.
Để chứng minh ( A); ( B ) luôn cắt nhau.
Ta chứng minh:
| OA - OB | < AB < OA + OB
+) Chứng minh: | OA - OB | < AB
Ta có: OA\(^2\)+ OB \(^2\)- 2OA . OB < AB \(^2\)
<=> OA\(^2\)+ OB \(^2\)- 2OA . OB < OA \(^2\)+ OB\(^2\)
<=> -2 OA. OB < 0 luôn đúng
Vậy | OA - OB | < AB
+) AB < OA + OB luôn đúng xét trong tam giác OAB
Vậy ( A); ( B) luôn luôn cắt nhau