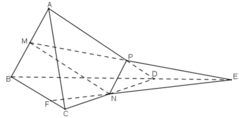
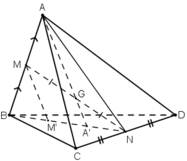
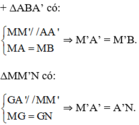1) . Cho tứ diện ABCD. gọi E và F lần lượt là trung điểm của AD, CD, G trên đoạn AB sao cho GA=2GB
a) Tìm M=GE giao mp(BCD).
b) Tìm H=BC giao(EFG). Suy ra thiết diện của (EFG) với tứ diện ABCD. Thiết diện là hình gì?
c) Tìm (DGH) giao (ABC).
d) chứng minh: EF//(ABC).