Một tủ sách có 36 quyển sách được phân thành 3 loại Toán, Lý, Hóa. Biết số quyển sách Toán ít hơn số quyển sách Lý 2 quyển; tổng số quyển sách Toán và Hóa gấp đôi số quyển sách Lý. Hỏi số lượng quyển sách từng loại Toán, Lý Hóa là bao nhiêu?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
5 tháng 1 2019
Đáp án C
Phương pháp.
Sử dụng định nghĩa của xác suất.
Lời giải chi tiết.
Tổng số sách là 4 + 3 + 2 = 9. Số cách lấy 3 quyển sách là C 9 3 = 84 (cách).
Số quyển sách không phải là sách toán là 3 + 2 = 5
Số cách lấy 3 quyển sách không phải là sách toán là C 5 3 = 10 (cách).
Do đó số cách lấy được ít nhất một quyển sách toán là 84 - 10 = 74 (cách).
Vậy xác suất để lấy đượcc ít nhất một quyển là toán là 74 84 = 37 42
CM
3 tháng 10 2019
Đáp án C
Lấy ngẫu nhiên 3 cuốn sách có: C 9 3 = 84 cách
Gọi A là biến cố: Lấy 3 cuốn sách và không có cuốn nào là cuốn toán
Suy ra A ¯ là biến cố: 3 quyển được lấy ra có ít nhất một quyển là toán
Khi đó Ω A = C 5 3 = 10 .
Vậy p A = Ω A Ω = 10 84 = 5 42 ⇒ p A ¯ = 1 − p A = 37 42
CM
29 tháng 4 2019
Đáp án A
Tổng số quyển sách trên giá là: 4 + 3 + 2 = 9 (quyển).
Số cách lấy ra 3 quyển sách từ 9 quyển sách đó là: C 9 3 .
Số cách lấy ra 3 quyển sách trong đó không có quyển sách toán nào là: C 5 3 .
Xác suất để 3 quyển được lấy ra có ít nhất một quyển là toán là C 9 3 − C 5 3 C 9 3 = 37 42
CM
8 tháng 12 2019
Đáp án A
Tổng số quyển sách trên giá là: 4 + 3 + 2 = 9 (quyển).
Số cách lấy ra 3 quyển sách từ 9 quyển sách đó là: C 9 3 .
Số cách lấy ra 3 quyển sách trong đó không có quyển sách toán nào là: C 5 3 .
Xác suất để 3 quyển được lấy ra có ít nhất một quyển là toán là C 9 3 - C 5 3 C 9 3 = 37 42
CM
23 tháng 5 2018
Đáp án C
Lấy ngẫu nhiên 3 cuốn sách có: C 9 3 = 84 cách
Gọi A là biến cố:
Lấy 3 cuốn sách và không có cuốn nào là cuốn toán
Suy ra A ¯ là biến cố:
3 quyển được lấy ra có ít nhất một quyển là toán
Khi đó Ω A = C 5 3 = 10
Vậy P A = Ω A Ω = 5 42
⇒
p
A
¯
=
1
-
p
A
=
37
42
CM
19 tháng 8 2017
Đáp án C
Phương pháp giải: Sử dụng biến cố đối và các quy tắc đếm cơ bản.
Lời giải:
Chọn 3 quyển sách trong 15 quyển sách có 
cách => n(Ω) = 455
Gọi X là biến cố 3 quyển sách được lấy ra có ít nhất một quyển sách là toán.
Và X là biến cố 3 quyển sách được lấy ra không có quyển sách toán. Khi đó, ta xét các trường hợp sau:
TH1. Lấy được 2 quyển lý, 1 quyển hóa => có 
cách
TH2. Lấy được 1 quyển lý, 2 quyển hóa => có 
cách
TH3. Lấy được 3 quyển lý, 0 quyển hóa => có 
cách
TH4. Lấy được 0 quyển lý, 3 quyển hóa => có 
cách
Suy ra số phần tử của biến cố
X
là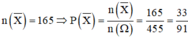 
Vậy xác suất cần tính là 
CM
12 tháng 3 2019
Đáp án C
Phương pháp giải: Sử dụng biến cố đối và các quy tắc đếm cơ bản.
Lời giải:
Chọn 3 quyển sách trong 15 quyển sách có C 15 3 = 455 cách ⇒ n ( Ω ) = 455
Gọi X là biến cố 3 quyển sách được lấy ra có ít nhất một quyển sách là toán.
Và X là biến cố 3 quyển sách được lấy ra không có quyển sách toán. Khi đó, ta xét các trường hợp sau:
TH1. Lấy được 2 quyển lý, 1 quyển hóa => có C 5 2 . C 6 1 = 60 cách
TH2. Lấy được 1 quyển lý, 2 quyển hóa => có C 5 1 . C 6 2 = 75 cách
TH3. Lấy được 3 quyển lý, 0 quyển hóa => có C 5 3 . C 6 0 = 10 cách
TH4. Lấy được 0 quyển lý, 3 quyển hóa => có C 5 0 . C 6 3 = 20 cách
Suy ra số phần tử của biến cố X là
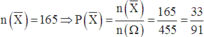
Vậy xác suất cần tính là
