Cho tam giác ABC vuông tại A có BC = 10cm. Gọi M; N lần lượt là trung điểm của AB; AC
a) Chứng minh MN song song với BC
b) Tính độ dài MN
AI GIẢI NHANH VÀ ĐÚNG MIK SẼ TICK
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A

Giải
a, Do AM là đường trung tuyến ứng với cạnh huyền của ΔABC vuông tại A, nên
AM = BM = CM = BC/2 = 10/2 = 5 (cm)
b, Do D là điểm đối xứng của A qua M nên AD = 2AM = 2BM = BC.
Do tứ giác ABDC có hai đường chéo AD và BC bằng nhau, cắt nhau tại trung điểm mỗi đường nên ABDC là hình chữ nhật ( dấu hiệu nhận biết hình chữ nhật )
c, Hình chữ nhật ABDC là hình vuông ⇔ ∡BMA = 90º
⇔ AM ⊥ BC
ΔABC có AM vừa là đường cao, vừa là đường trung tuyến nên ΔABC là tam giác cân tại A, kết hợp với ∡A = 90º ⇒ ΔABC vuông cân tại A.
Vậy với ΔABC vuông cân tại A thì tứ giác ABDC là hình vuông.

Vì M là trung điểm của AB nên:
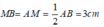
Áp dụng định lí py tago vào tam giác ABC có:
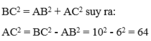
Suy ra: AC = 8cm
Xét tam giác ABC có M và N lần lượt là trung điểm của AB và BC nên MN là đường trung bình của tam giác ABC nên: MN// AC và
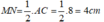
Suy ra: tứ giác MNCA là hình thang vuông.
Diện tích hình thang MNCA là:
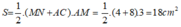
Chọn đáp án D

a) Xét tam giác ABC có:
BC2 = 102 = 100 (cm)
AB2 + AC2 = 62 + 82 = 36 + 64 = 100 (cm)
=> BC2 = AB2 + AC2 (= 100)
=> Tam giác ABC vuông tại A (định lý Pytago đảo)
b) MB = MD (gt) => M là trung điểm BD
Xét Tứ giác ABCD có:
M là trung điểm của BD (cmt)
M là trung điểm của AC (gt)
=> ABCD là hình bình hành (dhnb)
=> AB // CD (Tính chất hình bình hành)

a: Xét ΔABC có AB<AC<BC
nên góc C<góc B<góc A
b: Xét ΔCDB có
CA,DK là trung tuyến
CA cắt DK tại M
=>M là trọng tâm
=>CM=2/3CA=16/3(cm)
c: Gọi giao của d với AC là N
d là trung trực của AC
=>d vuông góc AC tại N và N là trung điểm của AC
=>QN//AD
Xét ΔCAD có
N là trung điểm của AC
NQ//AD
=>Q là trung điểm của CD
Xét ΔCDB có
BQ là trung tuyến
M là trọng tâm
=>B,M,Q thẳng hàng
a, Ta có: AB < AC < BC
=> C < B< A
b, Xét tam giác BCD có CA và DK là đường trung tuyến
CA cắt DK tại M
=> M là trọng tâm tam giác BCD
=> MC= 2/3 AC= 2/3.8= 16/3 cm
c, Xét tam giác ABC và tam giác ADC có:
AB = AD
BAC= DAC= 90°AC chung
=> tam giác ABC = tam giác ADC (c.g.c)
=> ACB= ACD (2 góc tương ứng) và BC = DC ( 2 cạnh tương ứng) (1)
KQ là đường trung trực của AC
=> KQ vuông góc với AC tại E
Xét tam giác KCE và tam giác QCE có:
KCE= QCE
EC chung
KEC= QEC=90°
=> tam giác KCE = tam giác QCE (gcg)
=> KC = QC (2 cạnh tương ứng) (2)
Mà K là trung điểm BC (3)
Từ (1), (2) và (3) suy ra Q là trung điểm của DC
Xét tam giác BCD có M là trong tâm
=> M thuộc đường trung tuyến BQ
=> B, M, Q thẳng hàng

a: AC=8cm
Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ABDC là hình chữ nhật
Suy ra: \(\widehat{ABD}=90^0\)
b: Xét ΔAMB và ΔDMC có
MA=MD
MB=MC
AB=DC
Do đó: ΔAMB=ΔDMC
Xét ΔABC và ΔBAD có
BA chung
BC=AD
AC=BD
Do đó: ΔABC=ΔBAD
c: Xét tứ giác AEDF có
AE//DF
AE=DF
Do đó AEDF là hình bình hành
Suy ra: HAi đường chéo AD và EF cắt nhau tại trung điểm của mỗi đường
mà M là trung điểm của AD
nên M là trung điểm của FE
hay F,M,E thẳng hàng

a: \(AC=5\sqrt{3}\left(cm\right)\)
b: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
Suy ra: BA=BE
hay B nằm trên đường trung trực của AE(1)
Ta có: ΔABD=ΔEBD
nên DA=DE
nên D nằm trên đường trung trực của AE(2)
Từ (1) và (2) suy ra BD⊥AE
a)ta có MA=MB
NA=NC
=)MN là đường trung bình tam giác ABC
=)MN//BC
b)ta có MN là đường trung bình tam giác ABC (cmt)
=)MN=1/2BC
lại có BC = 10cm (gt)
=)MN=BC/2=5 cm
B A C M N
a) Xét tam giác ABC có :
M là trung điểm của AB
N là trung điểm của AC
=> MN là đường trung bình của tam giác ABC ( định nghĩa )
=> MN // BC ( tính chất )
b) Vì MN là trung bình của tam giác ABC ( chứng minh trên )
\(\Rightarrow MN=\frac{BC}{2}=\frac{10}{2}=5\left(cm\right)\) ( tính chất )