Tìm số hạng chứa x8 trong khai triển: M(x)= (1+x3(1-x5))8
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn A
(
1
+
x
+
x
2
+
x
3
)
10
![]()
![]()
![]()
Ta có các cặp (k;m): 2k + m = 5
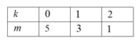
Suy ra hệ số của số hạng chứa
x
5
là: ![]()

Chọn C
Ta có ![]()
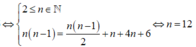 .
.
Xét khai triển 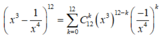
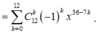 .
.
Số hạng chứa x 8 tương ứng với 36 - 7k = 8 => k = 4.
Vậy hệ số của số hạng chứa
x
8
trong khai triển
x
3
-
1
x
4
n
bằng ![]() .
.

Chọn đáp án A
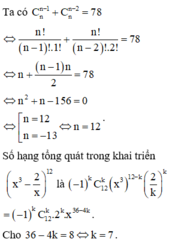
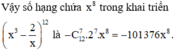
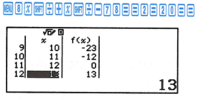
Lưu ý: Ta có thể xác định n bằng MTCT CASIO fx–580 VN X như sau:





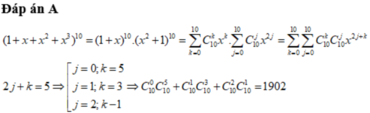
\(M=\sum\limits^8_{k=0}C_8^kx^{3k}\left(1-x^5\right)^k=\sum\limits^8_{k=0}C_8^kx^{3k}\sum\limits^k_{i=0}\left(-1\right)^i.x^{5i}=\sum\limits^8_{k=0}\left(\sum\limits^k_{i=0}C_{10}^kC_k^i\left(-1\right)^i.x^{3k+5i}\right)\)
Do \(\left\{{}\begin{matrix}0\le i\le k\le8\\3k+5i=8\\i;k\in N\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}i=1\\k=1\end{matrix}\right.\)
\(\Rightarrow\) Số hạng chứa \(x^8\) là: \(C_{10}^1.C_1^1.\left(-1\right)^1.x^8=-10x^8\)