cho 2 dường thẳng cắt nhau trong 4 góc tạo thành 1 góc = 50 độ
a) hãy kể tên các cặp góc đối đỉnh
b) tính các số đo còn lại
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 8 2023
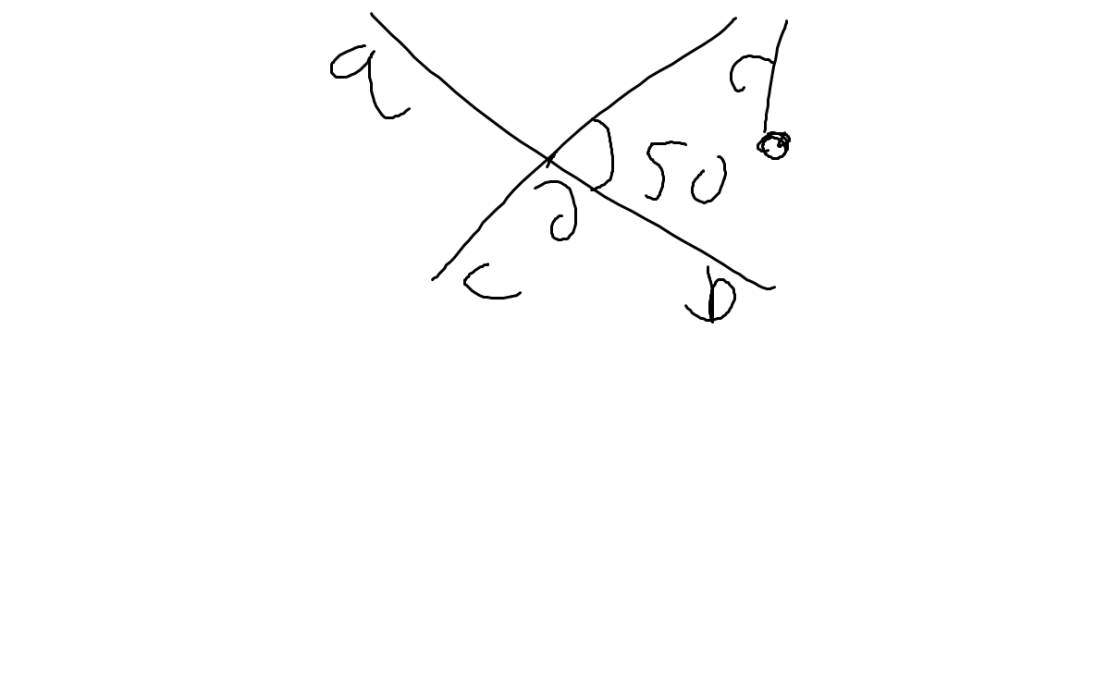
Gọi hai đường thẳng đề bài cho là ab và cd. Gọi O là giao của ab và cd
a: góc bOd và góc aOc
góc aOd và góc bOc
b: góc aOc=góc bOd=50 độ
góc aOd=góc bOc=180-50=130 độ
24 tháng 8 2017
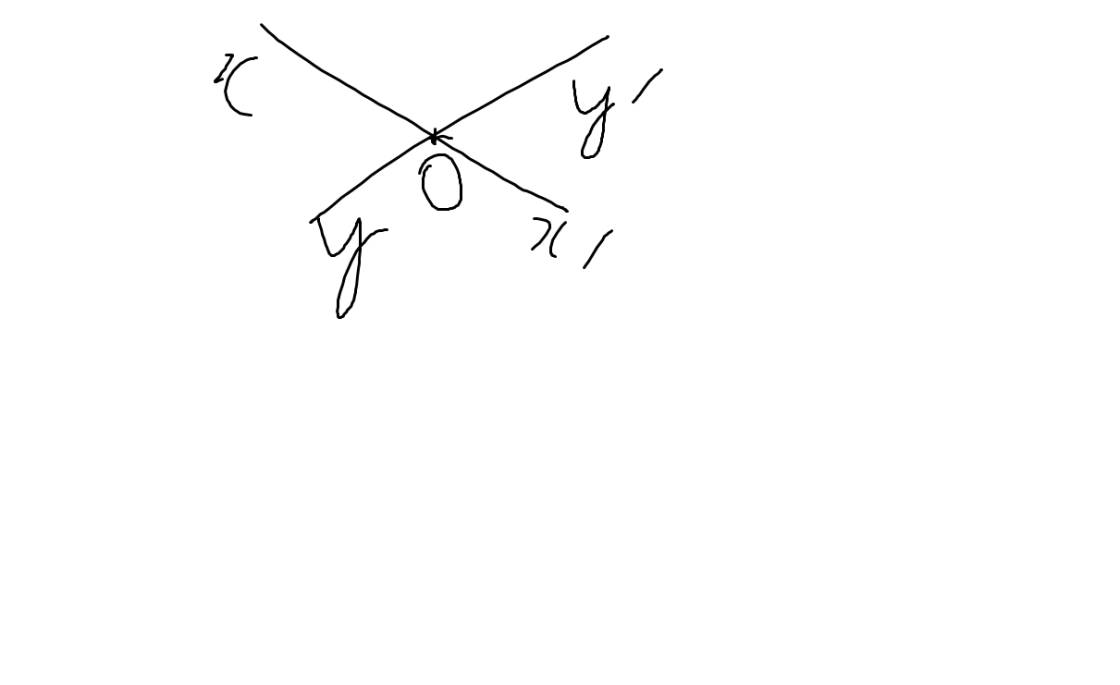
Gọi hai đường thẳng cắt nhau là xx' và yy'. Gọi điểm cắt giữa hai đường thẳng là O
a/ Các cặp góc đối đỉnh là: góc xOy đối đỉnh với góc y'Ox' ; góc x'Oy đối đỉnh với góc xOy'
b/ Gọi góc xOy = 50o
Vì góc xOy đối đỉnh với góc y'Ox'
suy ra góc xOy = y'Ox' = 50o
Vì hai đường thẳng xx' và yy' cắt nhau tại O
Suy ra tia Ox và tia Ox' đối nhau ; tia Oy và tia Oy' là hai tia đối nhau
Suy ra góc xOy và góc yOx' kề bù
Suy ra góc xOy + góc yOx' = 180o
50o + góc yOx' = 180o ( vì góc xOy = 50o )
góc yOx' = 180o - 50o = 130o
Vì góc yOx' và góc xOy' là hai góc đối đỉnh
Suy ra góc yOx' = góc xOy' = 130o
Vậy: ........... ( bạn tự viết nhé )
Nhớ k cho mình nhé! Thank you!!!
21 tháng 8 2019
Ta có : \(\widehat{O_1}\)và \(\widehat{O_3}\) ( đối đỉnh )
\(\widehat{O_1}\) và \(\widehat{O_3}=130^o\left(gt\right)\)
\(\Rightarrow\widehat{O_1}=\widehat{O_3}=\frac{130^o}{2}=65^o\)
\(\widehat{O_2}=\widehat{O_4}=180^o-65^o=115^o\)
Chúc bạn học tốt !!!
18 tháng 6 2021
a) Vì góc MAP và NAQ là 2 góc đối đỉnh
=> MAP = NAQ = 42o
Vì MAP và MAQ là 2 góc kề bù
=> MAP + MAQ = 180o => MAQ = 180o - 42o = 138o
b) Các cặp góc đối đỉnh: MAP và NAQ ; MAQ và NAP
11 tháng 7 2019
Giả sử hai đường thẳng \(xx'\)và \(yy'\)cắt nhau tại O và \(\widehat{xOy}=47^0\)
\(\Rightarrow\widehat{x'Oy'}=\widehat{xOy}=47^0\)đối đỉnh
\(\widehat{xOy'}=180^0-\widehat{xOy}=180^0-47^0=133^0\)
do \(\widehat{xOy}\)và \(\widehat{xOy'}\)kề bù và \(\widehat{x'Oy}=\widehat{xOy'}=133^0\)
11 tháng 7 2019
Bài 2 : Ta có hình vẽ :
Các cặp góc bằng nhau là : \(\widehat{xOy}=\widehat{x'Oy'};\widehat{yOz}=\widehat{y'Oz'}\)
25 tháng 10 2023
1:
a: Hai cặp góc đối đỉnh là \(\widehat{xOy};\widehat{x'Oy'}\) và \(\widehat{xOy'};\widehat{x'Oy}\)
b: hai cặp góc bù nhau là:
\(\widehat{xOy};\widehat{xOy'}\)
\(\widehat{x'Oy};\widehat{x'Oy'}\)
KT
27 tháng 9 2018
a) Vì \(MOP-MOQ\) là hai góc kề bù, ta có :
\(MOQ=180^0_{ }-MOP=180^0_{ }-70^0_{ }\)
\(\Rightarrow MOQ=110^0_{ }\)
Áp dụng tính chất hai góc đối đỉnh, ta có :
\(MOP=NOQ\)
\(MOQ=PON\)
b) Vì \(Ot\) là tia phân giác của \(MOP\Rightarrow TOP=TOM=\frac{1}{2}MOP=\frac{110}{2}=55^0_{ }\)
Vì \(POT-QOT'\) là hai góc đối đỉnh \(\Rightarrow POT=QOT'=55^0_{ }\left(1\right)\)
Vì \(MOT-NOT'\)là hai góc đối đỉnh \(\Rightarrow MOT=NOT'=55^0_{ }\left(2\right)\)
Từ \(\left(1\right)-\left(2\right)\Rightarrow OT'\)là tia phân giác của \(NOQ\)
c) \(POT-QOT'\)
\(MOT-NOT'\)
\(POM-NOQ\)