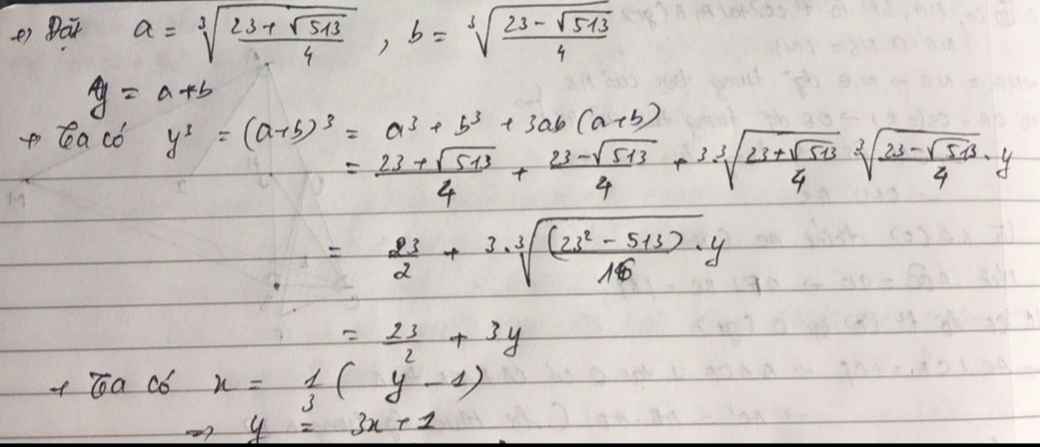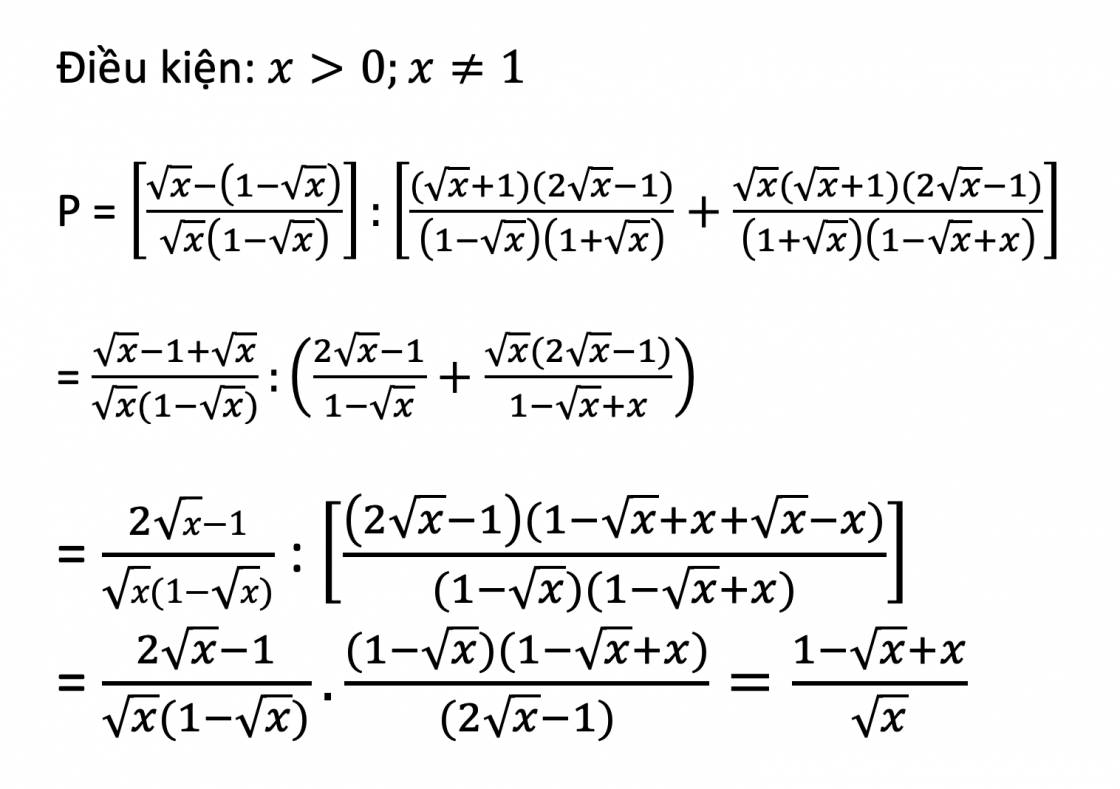\(\dfrac{1+2x}{1+\sqrt{1+2x}}\)+\(\dfrac{1-2x}{1-\sqrt{1-2x}}\) với x=\(\dfrac{\sqrt{3}}{4}\)
Tính giá trị biểu thức trên..
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 3 2022
Đặt \(y=\sqrt[3]{\dfrac{23+\sqrt{513}}{4}}+\sqrt[3]{\dfrac{23-\sqrt{513}}{4}}\) ( bạn lập phương cả 2 vế nhé )
\(\Leftrightarrow2y^3=6y+23\left(1\right)\)
theo đề bài,ta có: \(x=\dfrac{1}{3}\left(y-1\right)\)
\(\Leftrightarrow3x=y-1\Leftrightarrow y=3x+1\left(2\right)\Leftrightarrow2y^3=54x^3+54x^2+18x+2\left(3\right)\)
Thế (2) và (3) vào (1)
\(\Leftrightarrow54x^3+54x^2+18x+2=6\left(3x+1\right)+23\)
\(\Leftrightarrow54x^3+54x^2+18x+2=18x+6+23\)
\(\Leftrightarrow54x^3+54x^2=27\)
\(\Leftrightarrow2x^3+2x^2=1\)
\(A=2x^3+2x^2+1\)
\(A=1+1=2\)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 7 2021
\(x=\dfrac{\sqrt{3}\left(\sqrt{\sqrt{3}+1}+1-\sqrt{\sqrt{3}+1}+1\right)}{\left(\sqrt{\sqrt{3}+1}-1\right)\left(\sqrt{\sqrt{3}+1}+1\right)}=\dfrac{2\sqrt{3}}{\sqrt{3}+1-1}=2\)
\(\Leftrightarrow B=\left(2^4-2.2^3-2^2+2.2-1\right)^{2020}=\left(-1\right)^{2020}=1\)
12 tháng 7 2023
\(x=\sqrt{\dfrac{2\sqrt{3}+2-6\sqrt{3}}{2\sqrt{3}\left(2\sqrt{3}+2\right)}}=\sqrt{\dfrac{2-4\sqrt{3}}{2\sqrt{3}\left(2\sqrt{3}+2\right)}}\) ko tồn tại vì 2-4căn 3<0
5 tháng 1 2022
\(a,B=\dfrac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{1+\sqrt{x}}-\sqrt{x}\\ B=x-\sqrt{x}+1-\sqrt{x}=\left(\sqrt{x}-1\right)^2\)
Mà \(x=4-2\sqrt{3}=\left(\sqrt{3}-1\right)^2\)
\(\Rightarrow B=\left(\sqrt{3}-1-1\right)^2=\left(\sqrt{3}-2\right)^2=7-4\sqrt{3}\)
\(b,P=AB=\dfrac{2x+1-x+\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\left(\sqrt{x}-1\right)^2\\ P=\dfrac{\left(x+\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{x+\sqrt{x}+1}=\sqrt{x}-1\\ c,Q=\sqrt{x}+\dfrac{1}{P}=\sqrt{x}+\dfrac{1}{\sqrt{x}-1}\\ Q=\sqrt{x}-1+\dfrac{1}{\sqrt{x}-1}+1\ge2\sqrt{1}+1=3\\ Q_{min}=3\Leftrightarrow\left(\sqrt{x}-1\right)^2=1\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}-1=1\\1-\sqrt{x}=1\end{matrix}\right.\Leftrightarrow\sqrt{x}=2\left(x>1\Leftrightarrow\right)x=4\left(tm\right)\)
5 tháng 1 2022
a: \(B=\left(\sqrt{x}-1\right)^2=\left(\sqrt{3}-2\right)^2=7-4\sqrt{3}\)
b: \(A=\dfrac{2x+1-x+\sqrt{x}}{x\sqrt{x}-1}\cdot\left(\sqrt{x}-1\right)^2=\sqrt{x}-1\)
AT
8 tháng 7 2021
\(\sqrt{\dfrac{4}{2x+3}}\) xác định khi \(\dfrac{4}{2x+3}\ge0\Rightarrow2x+3>0\Rightarrow x>-\dfrac{3}{2}\)
\(\sqrt{\dfrac{2x-1}{2-x}}\) xác định khi \(\dfrac{2x-1}{2-x}\ge0\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}2x-1\ge0\\2-x>0\end{matrix}\right.\\\left\{{}\begin{matrix}2x-1\le0\\2-x< 0\end{matrix}\right.\left(l\right)\end{matrix}\right.\Rightarrow\dfrac{1}{2}\le x< 2\)
17 tháng 7 2021
a) Ta có: \(P=\left(\dfrac{\sqrt{x}+1}{\sqrt{2x}-1}+\dfrac{\sqrt{2x}+\sqrt{x}}{\sqrt{2x}+1}-1\right):\left(1+\dfrac{\sqrt{x}+1}{\sqrt{2x}+1}-\dfrac{\sqrt{2x}+\sqrt{x}}{\sqrt{2x}-1}\right)\)
\(=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{2x}+1\right)+\left(\sqrt{2x}+\sqrt{x}\right)\left(\sqrt{2x}-1\right)-2x+1}{\left(\sqrt{2x}-1\right)\left(\sqrt{2x}+1\right)}:\left(\dfrac{2x-1+\left(\sqrt{x}+1\right)\left(\sqrt{2x}-1\right)-\left(\sqrt{2x}+\sqrt{x}\right)\left(\sqrt{2x}+1\right)}{\left(\sqrt{2x}-1\right)\left(\sqrt{2x}+1\right)}\right)\)
\(=\dfrac{x\sqrt{2}+\sqrt{x}+\sqrt{2x}+1+2x-\sqrt{2x}+x\sqrt{2}+\sqrt{x}-2x+1}{2x-1}:\dfrac{2x-1+x\sqrt{2}-\sqrt{x}+\sqrt{2x}-1-\left(2x+\sqrt{2x}+x\sqrt{2}+\sqrt{x}\right)}{2x-1}\)
\(=\dfrac{2x\sqrt{2}+2\sqrt{x}+2}{-2-2\sqrt{x}}\)
10 tháng 7 2021
a) Ta có: \(M=\left(\dfrac{\sqrt{x}+1}{\sqrt{2x}+1}+\dfrac{\sqrt{2x}+\sqrt{x}}{\sqrt{2x}-1}-1\right):\left(1+\dfrac{\sqrt{x}}{\sqrt{2x}+1}-\dfrac{\sqrt{2x}+\sqrt{x}}{\sqrt{2x}-1}\right)\)
\(=\left(\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{2x}-1\right)+\sqrt{x}\left(\sqrt{2x}+1\right)^2-2x+1}{\left(\sqrt{2x}+1\right)\left(\sqrt{2x}-1\right)}\right):\left(\dfrac{2x-1+\sqrt{x}\left(\sqrt{2x}-1\right)-\sqrt{x}\left(\sqrt{2x}+1\right)^2}{\left(\sqrt{2x}+1\right)\left(\sqrt{2x}-1\right)}\right)\)
\(=\dfrac{x\sqrt{2}-\sqrt{x}+\sqrt{2x}-1+\sqrt{x}\left(2x+2\sqrt{2x}+1\right)-2x+1}{2x-1+x\sqrt{2}-\sqrt{x}-\sqrt{x}\left(2x+2\sqrt{2x}+1\right)}\)
\(=\dfrac{x\sqrt{2}-\sqrt{x}+\sqrt{2x}-2x+2x\sqrt{x}+2\sqrt{2x}+\sqrt{x}}{2x-1+x\sqrt{2}-\sqrt{x}-2x\sqrt{x}-2\sqrt{2x}-\sqrt{x}}\)
\(=\dfrac{x\sqrt{2}+3\sqrt{2x}-2x+2x\sqrt{x}}{x\sqrt{2}-2\sqrt{2x}+2x-2\sqrt{x}-2x\sqrt{x}}\)
23 tháng 12 2020
a) Ta có: \(P=\left(\dfrac{1}{\sqrt{x}-\sqrt{x-1}}-\dfrac{x-3}{\sqrt{x-1}-\sqrt{2}}\right)\left(\dfrac{2}{\sqrt{2}-\sqrt{x}}-\dfrac{\sqrt{x}+\sqrt{2}}{\sqrt{2x}-x}\right)\)
\(=\left(\dfrac{\sqrt{x}+\sqrt{x-1}}{x-\left(x-1\right)}-\dfrac{\left(\sqrt{x-1}-\sqrt{2}\right)\left(\sqrt{x-1}+\sqrt{2}\right)}{\sqrt{x-1}-\sqrt{2}}\right)\cdot\left(\dfrac{2}{\sqrt{2}-\sqrt{x}}-\dfrac{\sqrt{x}+\sqrt{2}}{\sqrt{x}\left(\sqrt{2}-\sqrt{x}\right)}\right)\)
\(=\left(\sqrt{x}+\sqrt{x-1}-\sqrt{x-1}-\sqrt{2}\right)\cdot\left(\dfrac{2\sqrt{x}}{\sqrt{x}\left(\sqrt{2}-\sqrt{x}\right)}-\dfrac{\sqrt{x}+\sqrt{2}}{\sqrt{x}\left(\sqrt{2}-\sqrt{x}\right)}\right)\)
\(=\left(\sqrt{x}-\sqrt{2}\right)\cdot\dfrac{2\sqrt{x}-\sqrt{x}-\sqrt{2}}{-\sqrt{x}\left(\sqrt{x}-2\right)}\)
\(=\left(\sqrt{x}-\sqrt{2}\right)\cdot\dfrac{\sqrt{x}-\sqrt{2}}{-\sqrt{x}\left(\sqrt{x}-2\right)}\)
\(=\dfrac{\sqrt{2}-\sqrt{x}}{\sqrt{x}}\)
b) Ta có: \(x=3-2\sqrt{2}\)
\(=2-2\cdot\sqrt{2}\cdot1+1\)
\(=\left(\sqrt{2}-1\right)^2\)
Thay \(x=\left(\sqrt{2}-1\right)^2\) vào biểu thức \(P=\dfrac{\sqrt{2}-\sqrt{x}}{\sqrt{x}}\), ta được:
\(P=\dfrac{\sqrt{2}-\sqrt{\left(\sqrt{2}-1\right)^2}}{\sqrt{\left(\sqrt{2}-1\right)^2}}\)
\(=\dfrac{\sqrt{2}-\left(\sqrt{2}-1\right)}{\sqrt{2}-1}\)
\(=\dfrac{\sqrt{2}-\sqrt{2}+1}{\sqrt{2}-1}\)
\(=\dfrac{1}{\sqrt{2}-1}\)
\(=\sqrt{2}+1\)
Vậy: Khi \(x=3-2\sqrt{2}\) thì \(P=\sqrt{2}+1\)