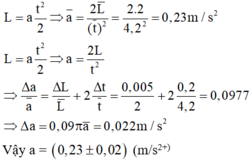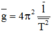Khi xác định gia tốc rơi tự do người ta sử dụng 1 thước đo milimet để đo quãng đường dài 50 cm và đồng hồ đo thời gian đi được quãng đường đó là 0,321 s. Biết rằng đồng hồ đang để ở thang đo 9,999s . Hãy viết kết quả gia tốc rơi tự do theo cả sai số tuyệt đối và sai số tỉ đối.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
26 tháng 9 2018
L = a t 2 2 ⇒ a ¯ = 2 L t 2 = 2 . 2 4 , 2 2 = 0 , 23 m / s 2
L = a t 2 2 ⇒ a = 2 L t 2 ⇒ ∆ a a = ∆ L L + 2 ∆ t t = 0 , 005 2 + 2 0 , 2 4 , 2 = 0 , 0977
⇒ ∆ a = 0 , 09 π . a ¯ = 0 , 022 m / s 2
Vậy a = (0,23 ± 0,02) ( m / s 2 )
VT
6 tháng 4 2018
Đáp án B
Ban đầu ta cần phải treo con lắc đơn lên giá tại nơi cần xác định gia tốc trọng trường g. Sau đó dùng thước đo 5 lần chiều dài l của dây treo từ điểm treo tới tâm vật. Tiếp theo kích thích cho vật nhỏ dao động, rồi dùng đồng hồ bấm giây để đo thời gian của một dao động toàn phần để tính được chu kỳ T, lặp lại phép đo 5 lần. Dựa vào công thức trung bình tính giá trị trung bình của chiều dài và chu kỳ sau đó thay vào công thức để tính gia tốc trọng trường trung bình tại ví trí đó.
1 tháng 11 2023
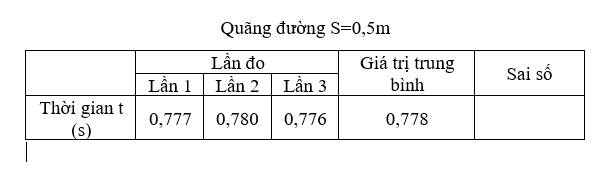
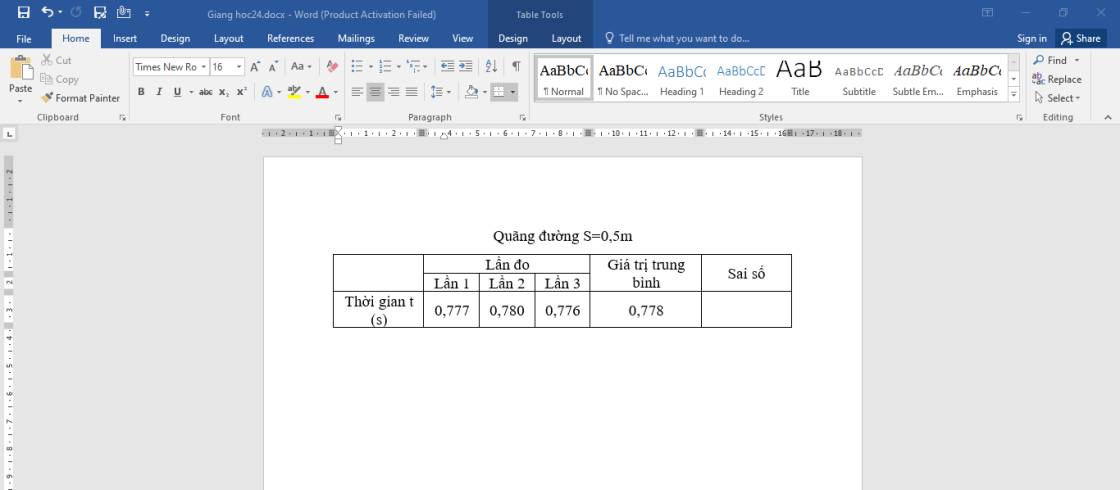
\(\overline{v}=\dfrac{s}{t}=\dfrac{0,5}{0,778}=\dfrac{250}{389}\approx0,643m/s\)
\(\overline{\Delta t}=\dfrac{\Delta t_1+\Delta t_2+\Delta t_3}{3}=\dfrac{\left|0,778-0,777\right|+\left|0,778-0,780\right|+\left|0,778-0,776\right|}{3}=\dfrac{1}{600}\)
\(\delta t=\dfrac{\overline{\Delta t}}{t}\cdot100\%;\delta s=\dfrac{\overline{\Delta s}}{s}\cdot100\%\)
\(\delta v=\delta s+\delta t=0,1\%\)
\(\Delta v=\delta v\cdot\overline{v}=0,1\%\cdot\dfrac{250}{389}\approx0,00064\)
Phép đo tốc độ trung bình là \(v=0,643\pm0,00064\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
17 tháng 9 2023
\(Tốc.độ.TB:\dfrac{35,2+36,15+35,75}{3}=35,7\left(s\right)\\ Sai.số.phép.đo:\dfrac{\left|35,7-35,2\right|+\left|35,7-36,15\right|+\left|35,7-35,75\right|}{3}\approx0,33\left(s\right)\\ Chọn.D\)