Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

| Công thức | Chuyển động thẳng đều | Chuyển động thẳng biến đổi đều | Chuyển động rơi tự do | Chuyển động ném ngang |
| Vận tốc | \(v=\frac{s}{t}\) | \(v=v_0+at\) | \(v=gt\) | \(v=\sqrt{v_0^2+g^2t^2}\) |
| Quãng đường (hoặc tầm bay xa) | \(s=vt\) | \(s=v_0t+\frac{1}{2}at^2\) | \(s=\frac{1}{2}gt^2\) | \(L=v_0\sqrt{\frac{2h}{g}}\) |
| Gia tốc | \(a=0\text{ m/s}^2\) | \(a=\frac{v-v_0}{t}\) | \(g\approx9,8\text{ m/s}^2\) | \(g\approx9,8\text{ m/s}^2\) |
| Thời gian chuyển động | \(t=\frac{s}{v}\) | \(----\) | \(t=\sqrt{\frac{2h}{g}}\) | \(t=\sqrt{\frac{2h}{g}}\) |

Bài làm:
a)Vận tốc trung bình trong 10 m đầu và 10 m thứ hai là:
v1 = v2 = \(\dfrac{s}{t_1}\) = \(\dfrac{10}{8}\) = 1,25(m/s)
Vận tốc trung bình trong 10 m thứ ba và 10 m thứ tư là:
v3 = v4 = \(\dfrac{s}{t_2}\) = \(\dfrac{10}{10}\) = 1(m/s)
Vận tốc trung bình trong ba quãng đường 10 m tiếp theo là:
v5 = v6 = v7 = \(\dfrac{s}{t_3}\) = \(\dfrac{10}{12}\) = \(\dfrac{5}{6}\)(m/s)
Vận tốc trung bình trong ba quãng đường 10 m cuối cùng là:
v8 = v9 = v10 = \(\dfrac{s}{t_4}\) = \(\dfrac{10}{14}\) = \(\dfrac{5}{7}\)(m/s)
b)Vận tốc trung bình trong cả quãng đường đi được là:
vtb = \(\dfrac{s'}{t}\) = \(\dfrac{s.10}{t_1.2+t_2.2+t_3.3+t_4.3}\) = \(\dfrac{10.10}{8.2+10.2+12.3+14.3}\) = \(\dfrac{50}{57}\)(m/s)
a) Áp dụng công thức tính vận tốc trung bình: \(v_{tb}=\dfrac{\Delta x}{\Delta t}\)
ta được:
vtb1 = 1,25 m/s; vtb2 = 12,5 m/s; vtb3= 1m/s; vtb4 = 1 m/s;
vtb5 = 0,83 m/s; vtb6= 0,83 m/s; vtb7= 0,83 m/s; vtb8= 0,71 m/s
vtb9 = 0,71 m/s; vtb10 = 0,71 m/s.
b)Vận tốc trung bình cho cả quãng đường:
\(v_{tb}=\dfrac{\Delta x}{\Delta t}=\dfrac{100}{114}=0,88m,s\)

a) Giá trị trung bình của thời gian rơi là:
\(\begin{array}{l}
\bar t = \frac{{{t_1} + {t_2} + {t_3} + {t_4} + {t_5}}}{5}\\
\Rightarrow \overline t = \frac{{0,2027 + 0,2024 + 0,2023 + 0,2023 + 0,2022}}{5} \approx 0,2024(s)
\end{array}\)
b)
- Sai số tuyệt đối ứng với 5 lần đo là:
+ Lần đo 1: \(\Delta {t_1} = \left| {\overline t - {t_1}} \right| = \left| {0,2024 - 0,2027} \right| = {3.10^{ - 4}}(s)\)
+ Lần đo 2: \(\Delta {t_2} = \left| {\overline t - {t_2}} \right| = \left| {0,2024 - 0,2024} \right| = 0(s)\)
+ Lần đo 3: \(\Delta {t_3} = \left| {\overline t - {t_3}} \right| = \left| {0,2024 - 0,2023} \right| = {10^{ - 4}}(s)\)
+ Lần đo 4: \(\Delta {t_4} = \left| {\overline t - {t_4}} \right| = \left| {0,2024 - 0,2023} \right| = {10^{ - 4}}(s)\)
+ Lần đo 5: \(\Delta {t_5} = \left| {\overline t - {t_5}} \right| = \left| {0,2024 - 0,2022} \right| = {2.10^{ - 4}}(s)\)
- Sai số tuyệt đối trung bình của phép đo thời gian là:
\(\overline {\Delta t} = \frac{{\Delta {t_1} + \Delta {t_2} + \Delta {t_3} + \Delta {t_4} + \Delta {t_5}}}{5} = \frac{{{{3.10}^{ - 4}} + 0 + {{2.10}^{ - 4}} + {{2.10}^{ - 4}} + {{10}^{ - 4}}}}{5} = 1,{6.10^{ - 4}}(s)\)

1.
Lập bảng ghi số liệu.
Độ dịch chuyển (m) | 0 | 200 | 400 | 600 | 800 | 1000 | 800 |
Thời gian (s) | 0 | 50 | 100 | 150 | 200 | 250 | 300 |
2.
Vẽ đồ thị:
Từ bảng số liệu ta vẽ được đồ thị như hình sau:


1.
a) Vẽ đồ thị độ dịch chuyển – thời gian:
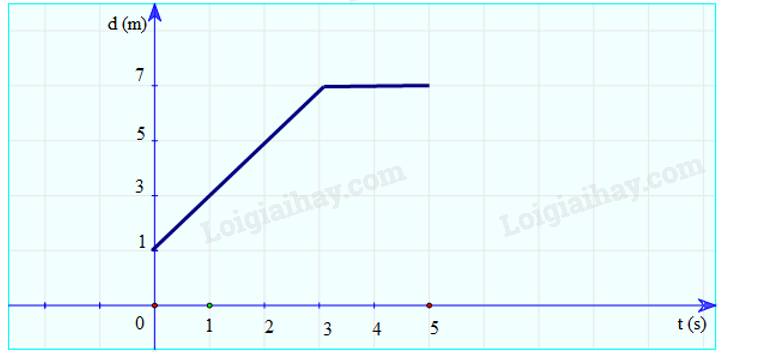
b) Mô tả chuyển động của xe:
- Từ 0 – 3 giây: xe chuyển động thẳng.
- Từ giây thứ 3 đến giây thứ 5: xe đứng yên (dừng lại)
c) Độ dịch chuyển của xe trong 3 giây đầu là:
\(d = 7 - 1 = 6m\)
Vận tốc của xe trong 3 giây đầu là:
\(v = \frac{{\Delta d}}{{\Delta t}} = \frac{6}{3} = 2\left( {m/s} \right)\)
2.
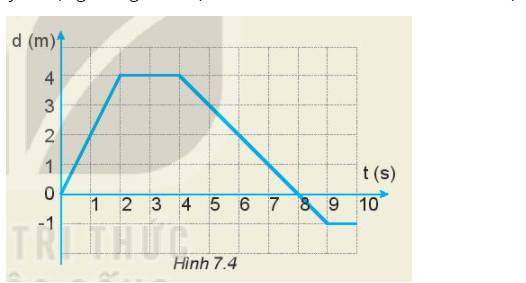
a) Mô tả chuyển động của xe:
- Trong 2 giây đầu: xe chuyển động thẳng
- Từ giây thứ 2 đến giây thứ 4: xe đứng yên
- Từ giây thứ 4 đến giây thứ 10: xe chuyển động thẳng theo chiều ngược lại.
- Từ giây thứ 9 đến giây thứ 10: xe dừng lại.
b)
- Ở giây thứ 2: xe ở vị trí cách điểm xuất phát 4 m.
- Ở giây thứ 4: xe ở vị trí cách điểm xuất phát 4 m
- Ở giây thứ 8: xe trở về vị trí xuất phát
- Ở giây thứ 10: xe ở vị trí cách điểm xuất phát 1 m theo chiều âm
c) Xác định tốc độ và vận tốc của xe:
- Trong 2 giây đầu, xe chuyển động thẳng, không đổi chiều nên tốc độ bằng vận tốc:
\(v = \frac{d}{t} = \frac{4}{2} = 2\left( {m/s} \right)\)
- Từ giây 2 đến giây 4: xe đứng yên nên vận tốc và tốc độ của xe đều bằng 0.
- Từ giây 4 đến giây 8:
+ Tốc độ: \(v = \frac{s}{t} = \frac{4}{4} = 1\left( {m/s} \right)\)
+ Vận tốc: \(v = \frac{{\Delta d}}{{\Delta t}} = \frac{{0 - 4}}{{8 - 4}} = - 1\left( {m/s} \right)\)
d)
- Từ đồ thị, ta thấy quãng đường đi được của xe sau 10 giây chuyển động là:
\(s = 4 + 4 + 1 = 9\left( m \right)\)
- Độ dịch chuyển của xe sau 10 giây là:
\(d = - 1 - 4 + 4 = - 1\left( m \right)\)
=> Quãng đường và độ dịch chuyển của xe sau 10 giây không giống nhau vì xe chuyển động theo 2 chiều.
\(Tốc.độ.TB:\dfrac{35,2+36,15+35,75}{3}=35,7\left(s\right)\\ Sai.số.phép.đo:\dfrac{\left|35,7-35,2\right|+\left|35,7-36,15\right|+\left|35,7-35,75\right|}{3}\approx0,33\left(s\right)\\ Chọn.D\)