cho R1ntR2, R1=6(ôm), hiệu điện thế toàn mạch là 12V, tính công suất cực đại của biến trở R2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Công suất mạch ngoài: \(P=I^2(R_1+R_2)\), mà \(I=\dfrac{E}{R_1+R_2+r}\)
\(\Rightarrow P= (\dfrac{E}{R_1+R_2+r})^2.(R_1+R_2)\), Đặt \(x=R_1+R_2\)
\(\Rightarrow P= (\dfrac{E}{x+r})^2.x=\dfrac{E^2x}{x^2+2xr+r^2}=\dfrac{E^2}{x+\dfrac{r^2}{x}+2r}\)
Pmax khi mẫu số min, mà \(x+\dfrac{r^2}{x}\ge 2\sqrt{x.\dfrac{r^2}{x}}=2r\)(dẫu '=' xảy ra khi \(x=r\))
Vậy \(P_{max}=\dfrac{E^2}{4r}=18W\), khi \(R_1+R_2=R \) \(\Rightarrow R_2=1,5\Omega\)
b. Làm tương tự
Công suất trên R2: \(P_2=I^2.R_2=(\dfrac{E}{R_1+r+R_2})^2.R_2\)
\(\Rightarrow P_2=\dfrac{E^2.R_2}{(R_1+r)^2+2.(R_1+r)R_2+R_2^2}\)
\(\Rightarrow P_2=\dfrac{E^2}{\dfrac{(R_1+r)^2}{R_2}+R_2+2.(R_1+r)}\)
P2 max khi mẫu số min, mà theo BĐT cô si ta có: \(\dfrac{(R_1+r)^2}{R_2}+R_2 \ge 2(R_1+r)\), dấu '=' xảy ra khi: \(\dfrac{(R_1+r)^2}{R_2}=R_2\)\(\Rightarrow R_2=R_1+r=2,5\Omega\)
\(P_{2max}=\dfrac{E^2}{4(R_1+r)}=14,4W\)

\(\dfrac{1}{R_{tđ}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}+\dfrac{1}{R_3}=\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{3}=1\Rightarrow R_{tđ}=1\Omega\)
\(U=U_1=U_2=U_3=12V\)
\(\left\{{}\begin{matrix}I=\dfrac{U}{R_{tđ}}=\dfrac{12}{1}=12\left(A\right)\\I_1=\dfrac{U_1}{R_1}=\dfrac{12}{2}=6\left(A\right)\\I_2=\dfrac{U_2}{R_2}=\dfrac{12}{6}=2\left(A\right)\\I_3=\dfrac{U_3}{R_3}=\dfrac{12}{3}=4\left(A\right)\end{matrix}\right.\)
\(\left\{{}\begin{matrix}P_3=U_3.I_3=4.12=48\left(W\right)\\P_m=U_m.I_m=12.12=144\left(W\right)\end{matrix}\right.\)

đề bài của bạn không rõ nhé, tức là ba điện trở mắc như nào, ba cái song song với nhau hay là 2 cái song song với 1 cái nối tiếp.Mình cũng muốn giúp nhưng đề ko rõ mình ko thể làm đc.Bạn có thể chỉ rõ mạch điện đc ko
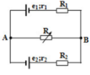
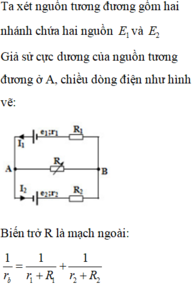
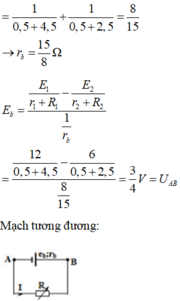

\(R1ntR2\Rightarrow P2=U2.I2=I2^2R2=Im^2.R2\)
\(\Rightarrow P2=\left(\dfrac{Um}{Rtd}\right)^2.R2=\left(\dfrac{12}{R1+R2}\right)^2.R2\)
\(\Rightarrow P2=\dfrac{12^2.R2}{\left(R1+R2\right)^2}=\dfrac{144R2}{\left(6+R2\right)^2}=\dfrac{144}{\dfrac{\left(6+R2\right)^2}{\sqrt{R2}^2}}=\dfrac{144}{\left(\dfrac{6}{\sqrt{R2}}+\sqrt{R2}\right)^2}\)
\(\Rightarrow\left(\dfrac{6}{\sqrt{R2}}+\sqrt{R2}\right)^2\ge\left(2\sqrt{6}\right)^2\ge24\left(AM-GM\right)\)
\(\Rightarrow P2=\dfrac{144}{\left(\dfrac{6}{\sqrt{R2}}+\sqrt{R2}\right)^2}\le\dfrac{144}{24}\le6W\Rightarrow P2max=6W\)
\(dấu\) \("="\) \(xảy\) \(ra\Leftrightarrow\dfrac{6}{\sqrt{R2}}=\sqrt{R2}\Leftrightarrow R2=6\Omega\)