Các bạn giúp mình với nè !
Cho tam giác ABC vuông ở A,đường cao AH.Vẽ đường tròn tâm A bán kính AH.Kẻ các tiếp tuyến BM và CN với đường tròn tâm A (M,N khác H)
a)CMR : 3 điểm A,M,N thẳng hàng và MB.CN=AH^2
b)CMR : MN là tiếp tuyến của đường tròn đường kính BC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu hỏi của VRCT_Ran love shinichi - Toán lớp 9 - Học toán với OnlineMath
Em tham khảo tại đây nhé.

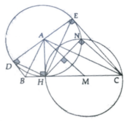
a, Chú ý: Ab là phân giác góc D A M ^ ; AC là phân giác góc E A M ^ từ đó D A E ^ = 180 0
b, Sử dụng tính chất hai tiếp tuyến và hệ thức về đường cao và hình chiếu cạnh góc vuông lên cạnh huyền trong tam giác vuông BAC => BD.CE = BH.CH = C H 2 = D E 2 4
c, ∆HNC nội tiếp đường tròn (M) đường kính HC => HN ⊥ NC
Chứng minh AN là tiếp tuyến của (M)
Do đó AM ⊥ HN => AM//NC

Tham khảo nè bn:
Câu hỏi của VRCT_Ran love shinichi - Toán lớp 9 - Học toán với OnlineMath

a: Xét (A) có
BD,BH là các tiếp tuyến
nên BD=BH và AB là phân giác của góc HAD(1)
Xét (A) có
CH,CE là các tiếp tuyến
nên CH=CE và AC là phân giác của góc HAE(2)
BH+CH=BC
=>BC=CE+BD
b: Từ (1), (2) suy ra góc DAE=2*90=180 độ
=>D,A,E thẳng hàng
c: Gọi M là trung điểm của BC
Xét hình thang BDEC có
M,A lần lượt là trung điểm của BC,DE
nên MA là đường trung bình
=>MA//CE//BD
=>MA vuông góc với BC
=>DE là tiếp tuyến của (M)

a: Xét (A) có
AH là bán kính
BH\(\perp\)AH tại H
CH\(\perp\)AH tại H
Do đó: BH,CH là tiếp tuyến có H là tiếp điểm
Xét (A) có
BH là tiếp tuyến có H là tiếp điểm
BM là tiếp tuyến có M là tiếp điểm
Do đó: AB là tia phân giác của \(\widehat{HAM}\)
Xét (A) có
CH là tiếp tuyến có H là tiếp điểm
CN là tiếp tuyến có N là tiếp điểm
Do đó: AC là tia phân giác của \(\widehat{HAN}\)
Ta có: \(\widehat{MAN}=\widehat{HAM}+\widehat{HAN}\)
\(=2\cdot\left(\widehat{BAH}+\widehat{CAH}\right)\)
\(=2\cdot90^0=180^0\)
Do đó: M,A,N thẳng hàng