Cho nửa đường tròn tâm O bán kính R,đường kính BC ,biết AB=R\(\sqrt{3}\)Tính AC và các góc của tam giác ABC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
5 tháng 12 2017
Đáp án C
Tam giác ABC có góc A là góc tù nên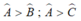 
Mà cạnh đối diện với góc A là cạnh BC .
Áp dụng định lí: trong 1 tam giác cạnh đối diện với góc lớn hơn thì lớn hơn ta được:
BC > AC và BC > AB
Vậy tam giác ABC có độ dài cạnh BC là lớn nhất nên dây BC gần tâm nhất.
Chưa thể kết luận dây nào xa tâm nhất.
AH
Akai Haruma
Giáo viên
3 tháng 3 2021
Lời giải:
$\widehat{BAC}=\frac{1}{2}\widehat{BOC}(1)$
$\widehat{BAC}=\frac{1}{2}(\text{sđc(BC)}-\text{sđc(MN nhỏ)})=\frac{1}{2}(\text{sđc(MB) nhỏ}+\text{sđc(NC) nhỏ})=\frac{1}{2}(\widehat{MIB}+\widehat{NIC})(2)$
Từ $(1);(2)\Rightarrow \widehat{MIB}+\widehat{NIC}=90^0$
$\Rightarrow \widehat{MIN}=90^0=\widehat{OIC}$
$\Rightarrow \widehat{MIO}=\widehat{NIC}$
$\Rightarrow \text{cung(MO)}=\text{cung(NC)}$
$\Rightarrow ONCM$ là hình thang cân (hệ quả quen thuộc)
$\Rightarrow MN=OC=R$
Ta có đpcm.