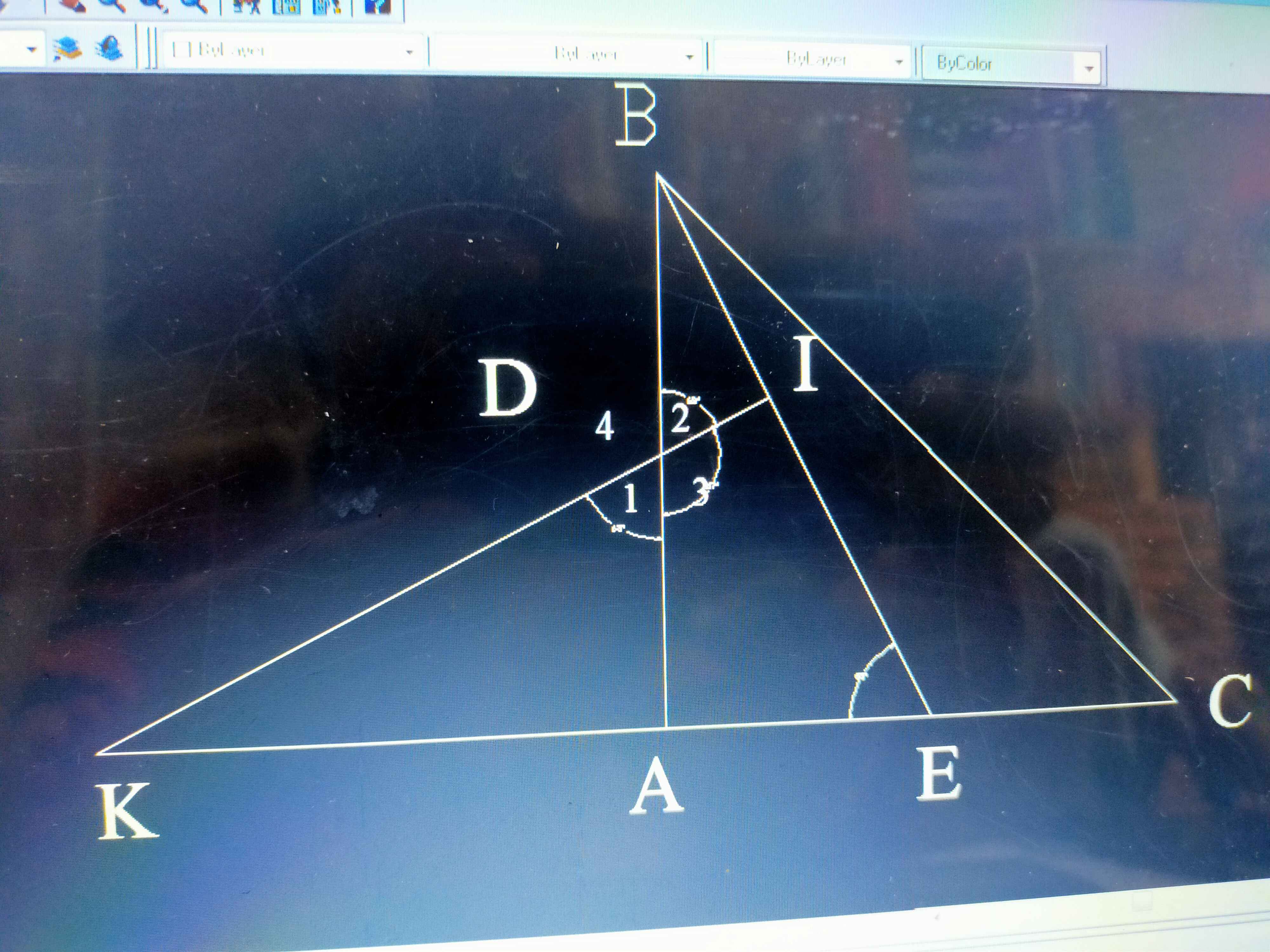
Cho tam giác ABC vuông tại A có AB=AC. Lấy D thuộc cạnh AB, điểm E thuộc cạnh AC sao cho AD=AE. Đường thẳng đi qua D vuông góc với DE cắt CA ở K. Chứng minh: AK=AC
(Vẽ hình nữa nha!!!!)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HN
5 tháng 6 2017
Xét hai tam giác KAD và BAE có:
\(\widehat{KAD}=\widehat{BAE}\left(=90^o\right)\)
AD = AE (gt)
\(\widehat{D_1}=\widehat{E_1}\) (cùng phụ với góc K)
Vậy: \(\Delta KAD=\Delta BAE\left(g-c-g\right)\)
Suy ra: AK = AB (hai cạnh tương ứng)
Ta lại có AB = AC
Do đó: AK = AC.
HK
28 tháng 8 2021
Xet tứ giác ADIE ta có: góc D3+ E =180
> D3=180- E.
> D4=180-D1
[ Góc D3 =D4 (đối đỉnh)]
>> góc D1= E.
xét tam giác ABE và tam giác KAD. Có góc D1=E, cạnh AD=AE,
---> Tam giác ABE = tam giác KAD.
-->> AB =AK
> AB=AC=KA
AK=AC.
>>
HL
12 tháng 11 2022
Xét tam giác BKE có: KG và BA là các đường cao => ED cũng là đường cao => ED vuông góc với BK.
Vì tam giác ABC vuông cân, AD = AE => DE //BC và góc ABC = 45 độ
=> BC vuông gocsvowis BK (vì DE vuông góc BK, BC // DE)
=> góc CBK = 90 độ => góc ABK = góc CBA - góc CBA = 90 - 45= 45.
Tam giác BKC có BA vừa là đường cao, vừa là phân giác => BKC cân => AC = AK (đpcm)